Förklaring av lösning
Hej
Jag behöver hjälp med att få en förklaring till denna lösning, någon har detta i en tråd (https://www.pluggakuten.se/trad/derivatan-av-y-c-a-x/) men jag förstår inte riktigt vad som händer här. Om jag även skulle kunna få en hänvisning till vilket av derivata kapitlen på matteboken.se detta handlar om skulle det vara hjälpsamt.
När man dricker kaffe tas koffein upp i blodet. Mängden koffein y, mg efter x, h kan beskrivas med formeln y=100⋅0,87^x
Med vilken hastighet minskar mängden koffein i blodet efter 2 h?
Mitt försök till lösning:
https://gyazo.com/abc090e0df22bdc6d6c772c65fbf8c7a
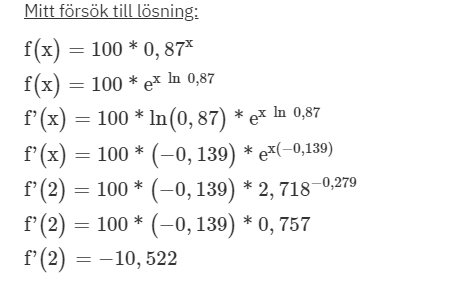
Svar: Efter 2 timmar minskar mängden koffein i blodet med 10,5 mg/h.
La in bilden åt dig /Smaragdalena, moderator
Mängden koffein y är en funktion av tiden x, dvs y(x).
Eftersom derivatan beskriver ändringshatigheten så är ändringshastigheten vid tidpunkten x lika med y'(x).
Du ska alltså derivera y(x) och sedan ta reda på derivatans värde vid tidpunkten x = 2 h.
Hur man deriverar en exponentialfunktion står i detta avsnitt av matteboken.se.
åh, då vet jag! tack så mycket för svaret!
Okej så jag förstår upp till det 3e steget i gyazo bilden. Jag kollade på videon i kapitlet och följde med där men jag förstår inte vad f'(x) = 100 * ln(0,87) * ex ln 0,87 betyder. Jag vet att e är ca 2,72 men förstår inte hur den naturliga logaritmen fungerar. Exemplet 3 = eln 3 visar sambandet men jag hänger ändå inte med- Sen förstår jag inte hur -0,139 kom med i bilden ! :(
f(x) = a^x
sättet man deriverar sådana funktioner gör man med hjälp av naturliga logaritmen som är VÄLDIG effektiv i och med att det har egenskapen att vara sin egen derivata.
a^x kan skrivas om med basen e, e^(x ln a)
precis som man skriver 3 = 10^lg 3 t.ex.
att derivera f(x) = a^x = e^x ln a gör man genom deriveringaregeln e^x ln a ➡️ ln a X e^x ln a
Förtydligande:
Eftersom så är
Efrersom så är
Eftersom derivatan av är lika med så är derivatan av lika med
.
Talet kommer in genom att
okej, dessa formler är riktigt svåra att förstå haha.. Hur blir ex(0,139) = 2,718-0,278?
Violett skrev:okej, dessa formler är riktigt svåra att förstå haha.. Hur blir ex(0,139) = 2,718-0,278?
Talet e är ungefär lika med 2,718.
Om du tittar i början av raden ser du att det de beräknar är f'(2), dvs derivatans värde då x = 2.
Om x = 2 så är exponenten x*(-0,139) = 2*(-0,139) = -0,278.


