Förhållande mellan strömmar

Jag förstår inte hur du räknade. Hur fick du 4/3? Kan du visa alla steg?

Laguna skrev:

Jag förstår inte hur du räknade. Hur fick du 4/3? Kan du visa alla steg?

Jag är väldigt osäker på om jag ens använde rätt metod för att få fram svaret, ursäkta om min handstil är dålig.

Hej!

Du ska räkna ut  kvoten $\frac{I_1}{I_2}$., eller hur?

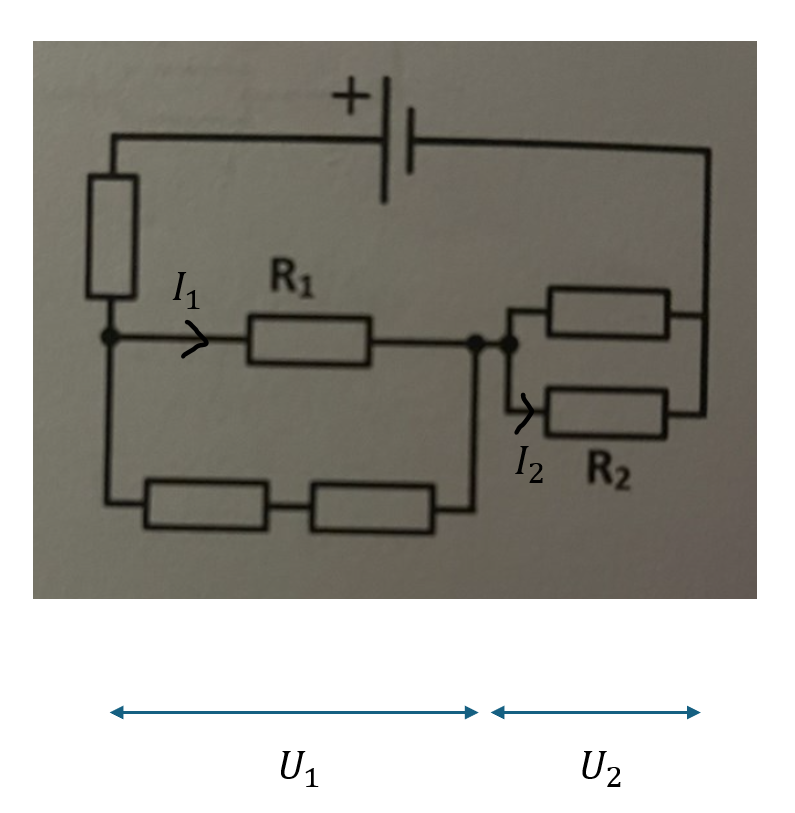
För att se hur man kan räkna ut kvoten så har jag infört ett par extra beteckningar i figuren. Kan du se hur du kan teckna svaret om du får använda dessa extra beteckningar?

JohanF skrev:

Hej!

Du ska räkna ut  kvoten $\frac{I_1}{I_2}$., eller hur?

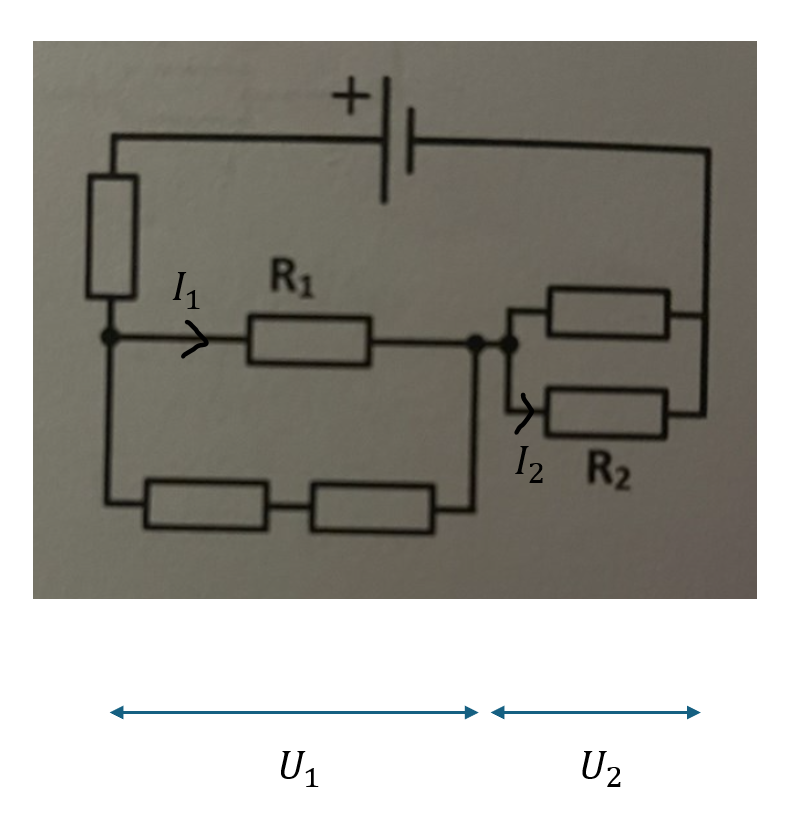
För att se hur man kan räkna ut kvoten så har jag infört ett par extra beteckningar i figuren. Kan du se hur du kan teckna svaret om du får använda dessa extra beteckningar?

 

nja, inte riktigt

Jag införde beteckningar för spänningarna över de två "delkretsarna" som du räknade ersättningsresistanserna för i ditt lösningsförsök. Det är för att lättare se hur vi ska komma vidare till rätt svar.

Om du tittar i figuren så ligger spänningarna $U_1$och $U_2$, överresistanserna $R_1$och $R_2$(vi kallar alla resistanser för $R$ hädanefter, eftersom det är givet i uppgiften). Alltså:

$\frac{I_1}{I_2}=\frac{U_1/R_1}{U_2/R_2}=\frac{U_1/R}{U_2/R}=\frac{U_1}{U_2}$

Alltså är strömkvoten $\frac{I_1}{I_2}$lika stor som spänningskvoten $\frac{U_1}{U_2}$, och vi kan räkna ut den kvoten istället.

Hänger du med?

JohanF skrev:

Jag införde beteckningar för spänningarna över de två "delkretsarna" som du räknade ersättningsresistanserna för i ditt lösningsförsök. Det är för att lättare se hur vi ska komma vidare till rätt svar.

Om du tittar i figuren så ligger spänningarna $U_1$och $U_2$, överresistanserna $R_1$och $R_2$(vi kallar alla resistanser för $R$ hädanefter, eftersom det är givet i uppgiften). Alltså:

$\frac{I_1}{I_2}=\frac{U_1/R_1}{U_2/R_2}=\frac{U_1/R}{U_2/R}=\frac{U_1}{U_2}$

Alltså är strömkvoten $\frac{I_1}{I_2}$lika stor som spänningskvoten $\frac{U_1}{U_2}$, och vi kan räkna ut den kvoten istället.

Hänger du med?

Jahaa, så spänningen i r1 kretsen är lika stor som spänningen i bara r1, och spänninge i r2 kretsen är lika stor som spänningen i bara r2`?

Ja! Ser du hur du kan beräkna spänningskvoten?

JohanF skrev:

Ja! Ser du hur du kan beräkna spänningskvoten?

tänker jag rätt nu?

Yesss!

JohanF skrev:

Yesss!

tack så mycket för hjälpen! :)

Kan du avgöra om det var en tillfällighet att du fick rätt svar i början?

Laguna skrev:

Kan du avgöra om det var en tillfällighet att du fick rätt svar i början?

Det var det nog, jag satt och tänkte hur jag skulle göra och det där visade sig vara det enda svaret som inte hade massa obekanta, men jag fattade inte hur jag fick fram svaret eller varför det var så, men nu gör jag det.

Enklast är det att bestämma strömmarna genom att använda strömdelning, http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmlaw.html#c3 

Så här:

punktfem3 skrev:

Laguna skrev:

Kan du avgöra om det var en tillfällighet att du fick rätt svar i början?

Det var det nog, jag satt och tänkte hur jag skulle göra och det där visade sig vara det enda svaret som inte hade massa obekanta, men jag fattade inte hur jag fick fram svaret eller varför det var så, men nu gör jag det.

Med tanke på resonemanget du förde var det en ren tillfällighet. Du hade med all säkerhet fått noll poäng på uppgiften, så jättebra att du kände att något var fel.

Jag tolkade dina beräkningar som att du gjorde två felaktiga antaganden.

1. Du antog att strömmarna I1 och I2 flöt genom de ersättningsresistanserna du beräknade. (När I1 och I2 per definition bara flyter genom R1 respektive R2)

2. Du antog att spänningarna över de två ersättningsresistanserna du beräknade är lika stora. (Vilket de skulle vara om de två ersättningsresistanserna var parallellkopplade. Men de i själva verket är seriekopplade)

Däremot spelade de två ersättningsresistanserna en avgörande roll för  det rätta svaret, vilket gjorde att svaren blev lika.