Förenkling av cos
Hej jag lyckas bara förenkla den andra termen, kan någon hjälpa mig med att förenkla första termen ? 
Kan du förenkla cos(90-x)?
Laguna skrev:Kan du förenkla cos(90-x)?
Det är det jag inte vet hur jag ska göra
Det är sin(x). Det borde stå någonstans i din bok.
user54321 skrev:Laguna skrev:Kan du förenkla cos(90-x)?
Det är det jag inte vet hur jag ska göra
Det borde stå i din bok, men en intuitiv anledning varför det stämmer är detta:
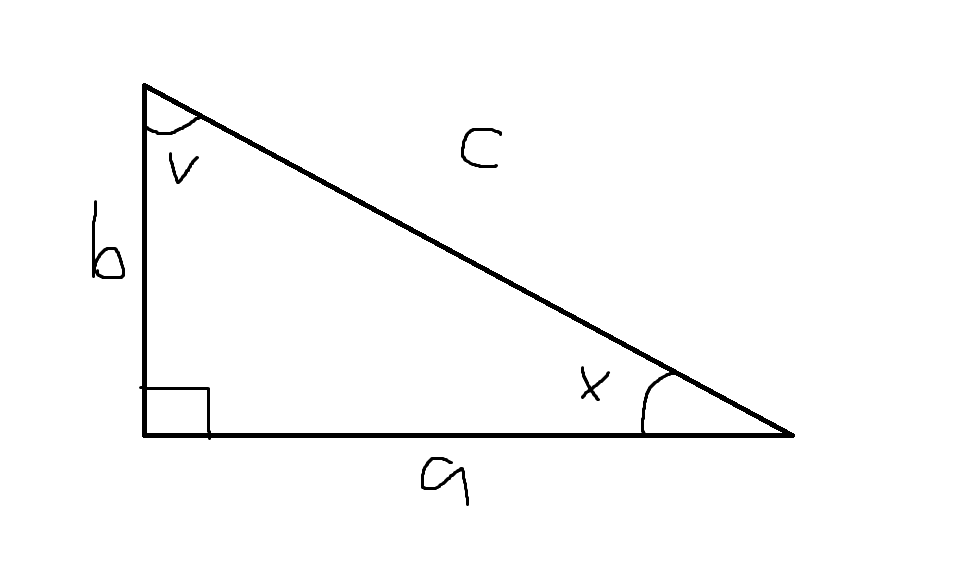 Från denna bild ser vi att och
Från denna bild ser vi att och
På samma sätt kan vi se att (närliggande / hypotenusa) och
Men eftersom vinkelsumman måste bli har vi att och då får vi att och
AlexMu skrev:user54321 skrev:Laguna skrev:Kan du förenkla cos(90-x)?
Det är det jag inte vet hur jag ska göra
Det borde stå i din bok, men en intuitiv anledning varför det stämmer är detta:
Från denna bild ser vi att och
På samma sätt kan vi se att (närliggande / hypotenusa) och
Men eftersom vinkelsumman måste bli har vi att och då får vi att och
Men i det här fallet är det ju cos(x-90) och inte
cos (90-x)
Då använder vi nästa regel: cos(v) = cos(-v).


