Förenkla
Uppgift: Förenkla sin(x+45°) - sin(x-45°)
Samband:
sin (u+v) = sinu*cosv + cosu*sinv
sin (u-v) = sinu*cosv- cosu * sinv
Min uträkning hittills:
sinx * cos45° + cosx * sin45° - (sinx * cos45° - cosx * sin45°) = 2cos*sin45
Min fråga är att jag har glömt bort hur jag ska förenklar termerna till att det blir 2cos* sin45. Kan någon förklara detta?
Hej och välkommen till Pluggakuten.
Om du tillfälligt kallar sin(x)•cos(45°) för a och cos(x)•sin(45°) för b så kan du skriva uttrycket på en mycket enklare form så här: a+b-(a-b).
Förenkla nu detta enklare uttryck och byt sedan tillbaka från a och b.
a+b-(a-b) = a+b - a+b = 2b
2b = cosx*sin45° + cosx*sin45° = 2cosx + sin45°^2
Vart gör jag fel någonstans?
Vilket värde har sin45o? Det skall du kunna utantill (eller åtminstone veta hur man tar fram det).
Ja det är väl sin 45° = 1/√2 ?
Men det jag inte förstår är hur det ska bli 2cos*sin45? Då det blir 2 stycken sin45 när jag räknat ovan?
Juliaanvändare skrev:a+b-(a-b) = a+b - a+b = 2b
2b = cosx*sin45° + cosx*sin45° = 2cosx + sin45°^2
Vart gör jag fel någonstans?
Det fetmarkerade ovan är fel.
Om b = cos(x)•sin(45°) så är 2b = 2•cos(x)•sin(45°)
Ah okej, tack! Blir svaret så pga detta?
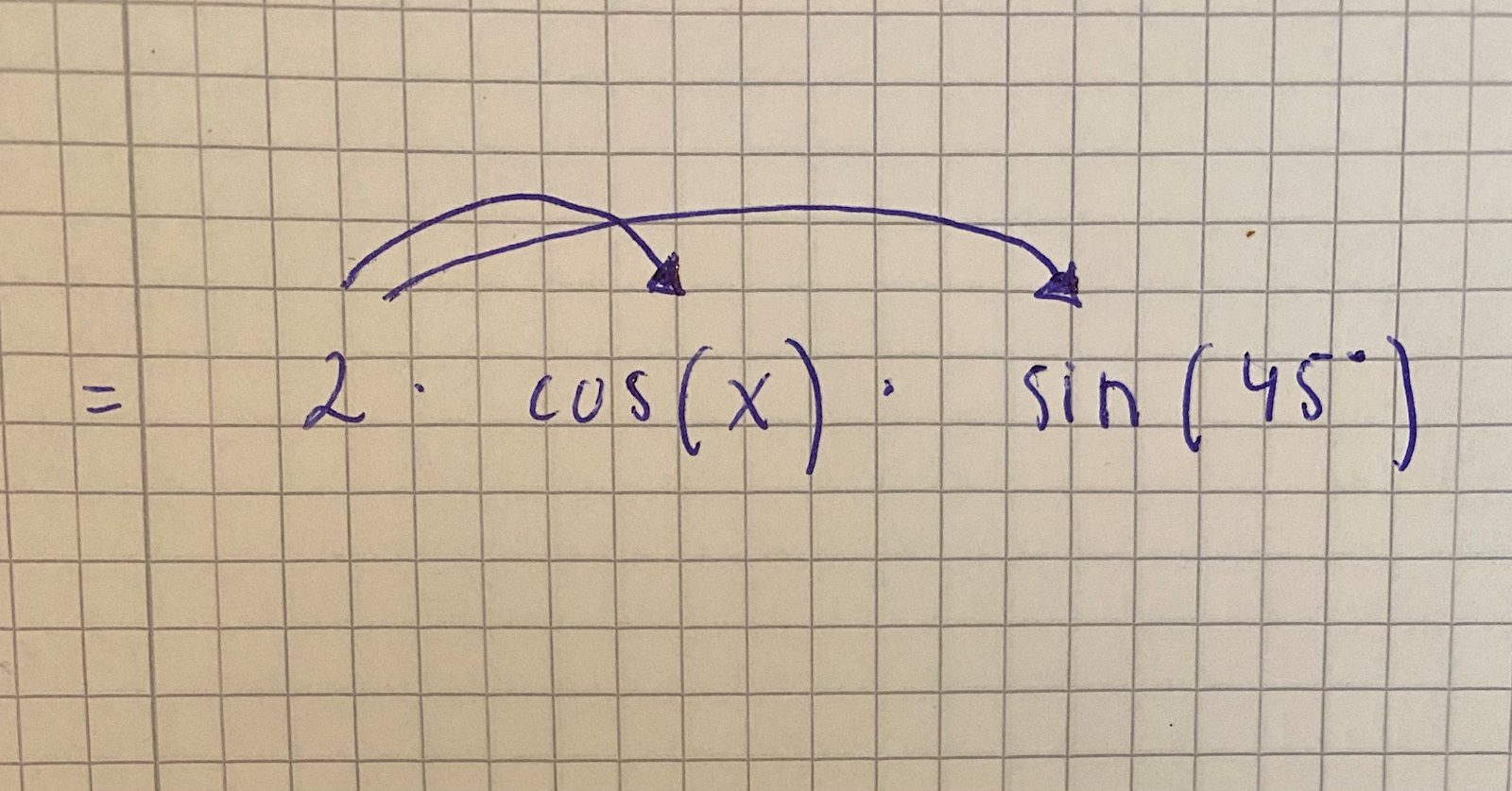
Jag förstår inte riktigt vad dina pilar betyder.
Vi tar ett konkret exempel.
Om b = 2•3 så är 2b = 2•(2•3) = 2•6 = 12.
Detta går även att beräkna på det sättet du började, nämligen 2b = 2•3+2•3 = 6+6 = 12.
Men det gäller inte som du skrev, att 2b = 2•3+2•3 = 2•3+32 = 6+9 = 15.
Yes nu hänger jag med! Tack så mycket för hjälpen!



