Före detta NP fråga i A-nivå

Hej!

Jag har problem med följande fråga:

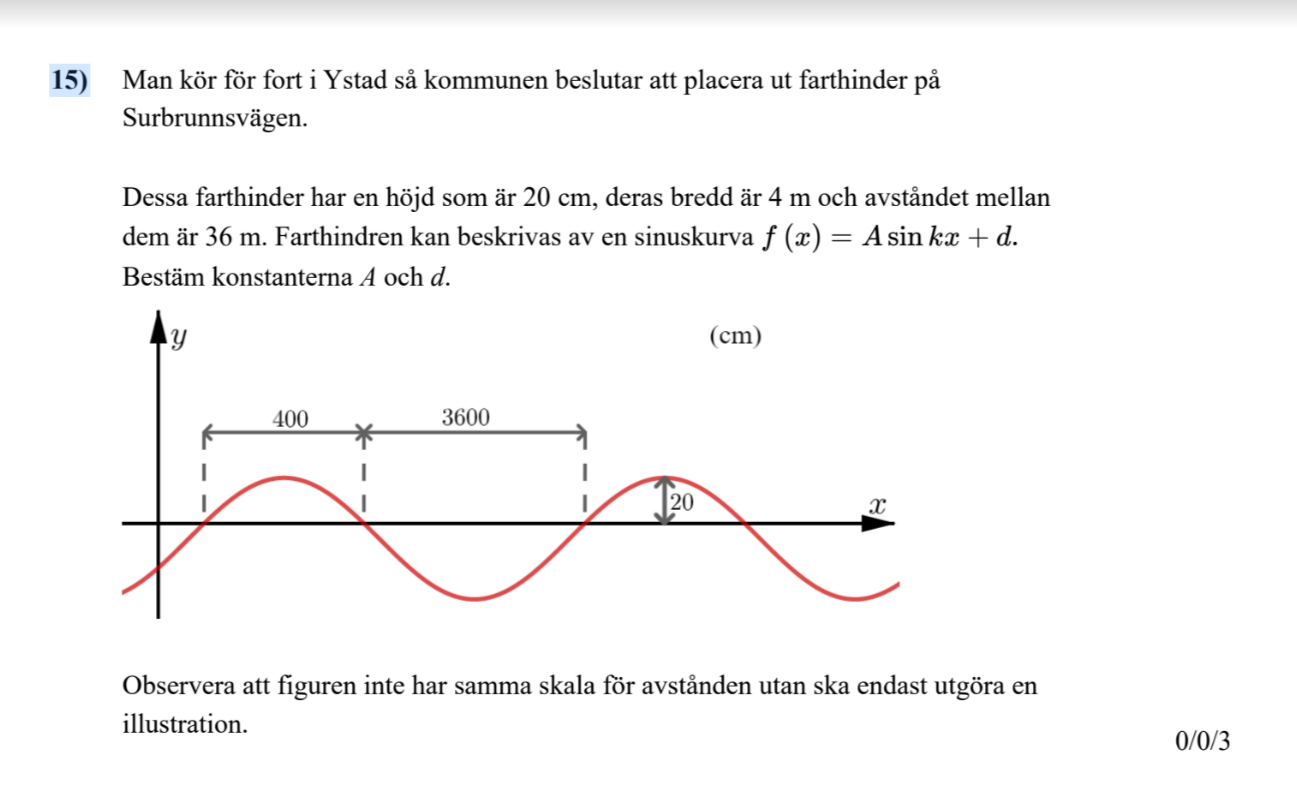Jag har ingen aning om hur jag ska börja. Det ända jag vet är att våglängden/perioden är 40 meter. Och inte i grader...

(mått i meter)

Givet att perioden är 40 rad måste $k = 2 π / 40 = π / 20$ rad. Nu har antalet okända minskats till två och uppgiften löses genom att ställa upp ett ekvationssystem med två ekvationer. Ekvationerna kan ställas upp utifrån informationen i uppgiften genom att dra nytta av att (1) avståndet mellan kurvans nollställen "runt samma topp" är 4, samt (2) att kurvans maximivärde är 0,2. Det är därför en bra idé att börja med att lösa ekvationen $f (x) = 0$ , skulle jag säga.

Lösning:

Visa spoiler

Först löses ekvationen $f (x) = 0$ , då fås lösningarna nedan.

$x_{1} = \frac{20}{π} \sin^{- 1} (- \frac{d}{A}) + 40 n x_{2} = 20 - \frac{20}{π} \sin^{- 1} (- \frac{d}{A}) + 40 n$

Ekvation 1 blir då

$|x_{2} - x_{1}| = 4 |20 - \frac{40}{π} \sin^{- 1} (- \frac{d}{A})| = 4 \sin^{- 1} (- \frac{d}{A}) = \frac{2 π}{5} - \frac{d}{A} = \sin (\frac{2 π}{5}) d = - A \sin (\frac{2 π}{5}) .$

Notera att steget där absolutbeloppet togs bort bygger på att differensen endast kan bli 4 om den andra termen är 16.

Nu gäller endast att lösa ut $A$ , vilket görs genom att ställa upp ekvation 2.

$m a x = 0, 2 0, 2 = A + d = A - A \sin (\frac{2 π}{5}) = A (1 - \sin (\frac{2 π}{5})) A = \frac{0, 2}{(1 - \sin (\frac{2 π}{5})) .}$

Insättning ger därmed

$d = - \frac{0, 2 \sin (\frac{2 π}{5})}{(1 - \sin (\frac{2 π}{5}))} .$

Hoppas det hjälper!

Anonymous75 skrev:
(mått i meter)

Givet att perioden är 40 rad måste $k = 2 π / 40 = π / 20$ rad. Nu har antalet okända minskats till två och uppgiften löses genom att ställa upp ett ekvationssystem med två ekvationer. Ekvationerna kan ställas upp utifrån informationen i uppgiften genom att dra nytta av att (1) avståndet mellan kurvans nollställen "runt samma topp" är 4, samt (2) att kurvans maximivärde är 0,2. Det är därför en bra idé att börja med att lösa ekvationen $f (x) = 0$ , skulle jag säga.

Lösning:

Visa spoiler

Först löses ekvationen $f (x) = 0$ , då fås lösningarna nedan.

$x_{1} = \frac{20}{π} \sin^{- 1} (- \frac{d}{A}) + 40 n x_{2} = 20 - \frac{20}{π} \sin^{- 1} (- \frac{d}{A}) + 40 n$

Ekvation 1 blir då

$|x_{2} - x_{1}| = 4 |20 - \frac{40}{π} \sin^{- 1} (- \frac{d}{A})| = 4 \sin^{- 1} (- \frac{d}{A}) = \frac{2 π}{5} - \frac{d}{A} = \sin (\frac{2 π}{5}) d = - A \sin (\frac{2 π}{5}) .$

Notera att steget där absolutbeloppet togs bort bygger på att differensen endast kan bli 4 om den andra termen är 16.

Nu gäller endast att lösa ut $A$ , vilket görs genom att ställa upp ekvation 2.

$m a x = 0, 2 0, 2 = A + d = A - A \sin (\frac{2 π}{5}) = A (1 - \sin (\frac{2 π}{5})) A = \frac{0, 2}{(1 - \sin (\frac{2 π}{5})) .}$

Insättning ger därmed

$d = - \frac{0, 2 \sin (\frac{2 π}{5})}{(1 - \sin (\frac{2 π}{5}))} .$

Hoppas det hjälper!

tack för svaret! Du gav svar på min studentdag, men ditt svar kommer säkert hjälpa framtida studenter!

Svara