För vilka värden på a är linjen en sekvent till kurvan?
Hej!
Jag håller på med denna uppgift som du kan se nedan. Nedan kan du även se hur jag har försökt lösa uppgiften. Problemet är att jag inte vet hur jag ska gå vidare härifrån och gärna hade velat ha hjälp med det! Kanske har jag gjort helt fel? Vad är det då för fel jag gör och varför är det fel? Vad ska jag då göra för att göra rätt? Jag uppskattar all hjälp!
Tack på förhand!


Att linjen är en sekant innebär att den sker på fler än ett ställe, eller hur?
Du har mycket korrekt satt de lika med varandra. Nu gäller det bara att hitta för vilka a det finns två skärningspunkter. Om det ska finnas två skärningspunkter måste diskriminanten>0, dvs:
Tillägg: 9 nov 2022 21:13
(Jag litar på att du har räknat rätt själv tills steget i slutet)
Rita så du får bättre förståelse för uppgiften.
naytte skrev:Att linjen är en sekant innebär att den sker på fler än ett ställe, eller hur?
Du har mycket korrekt satt de lika med varandra. Nu gäller det bara att hitta för vilka a det finns två skärningspunkter. Om det ska finnas två skärningspunkter måste diskriminanten>0, dvs:
Tillägg: 9 nov 2022 21:13
(Jag litar på att du har räknat rätt själv tills steget i slutet)
Okej då förstår jag!! Eftersom att diskriminanten blir 4 + a och inte får vara mindre än 0 så får a inte vara -4 och mindre. Därför blir svaret på frågan: a > -4. Stämmer det?
Tack för hjälpen!!
Om du grafar blir det mycket tydligare:
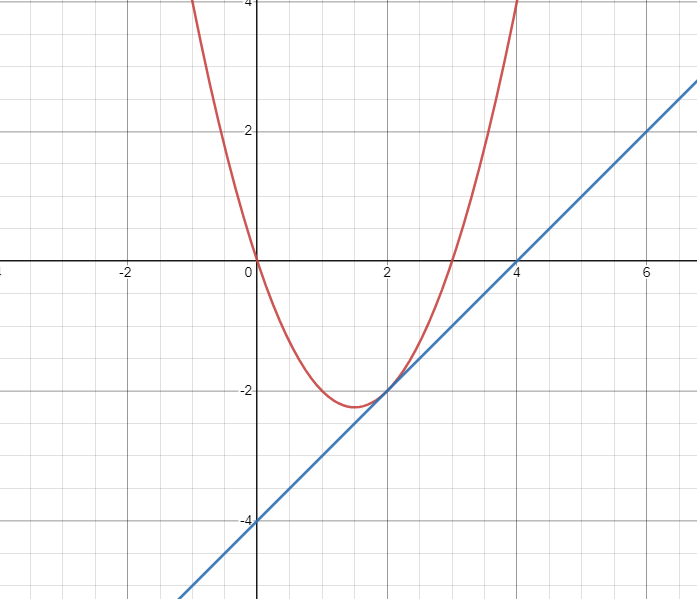
Här är a=-4. Då ser vi att linjen blir en tangent till parabeln, dvs. den skär exakt en gång. Om a ökar kommer antalet skärningspunkter också göra det. :)




