Flervariabelsanalys, trippelintegral

Har problem med att hitta integrationsgränserna. Har skrivit:
Tänkte att gränserna för z och x ser ut som ovan. Sedan testade jag att hitta skärningspunkterna mellan 2-2y och y^2 vilket gav -1-sqrt(3) och -1+sqrt(3) men när jag beräknat integralen några gånger nu blir det fel och antar att det är i gränserna felet finns.
Haraldo skrev:
Har problem med att hitta integrationsgränserna. Har skrivit:
Tänkte att gränserna för z och x ser ut som ovan. Sedan testade jag att hitta skärningspunkterna mellan 2-2y och y^2 vilket gav -1-sqrt(3) och -1+sqrt(3) men när jag beräknat integralen några gånger nu blir det fel och antar att det är i gränserna felet finns.
Har du följt instruktionerna och ritat upp området?
Det svåra här är att bestämma området och att rita det 3D utan program…
Vi har att 0 ≤ z ≤ 2-2y^2 och 0 ≤ x ≤ 2-z.
z ≤ 2-2y^2 ger oss att 2y^2 ≤ 2-z d.v.s. y^2 ≤ 1-z/2. Då z≥0 är högerledet ≤1 och vi har olikheten y^2≤1 vilket ger -1≤y≤1.
Vi kan nu skriva upp integralen
INT_{y=-1}^1 INT_{z=0}^{2-2y^2} INT_{0}^{2-z} x dx dz dy
Klarar du det därifrån?
Notera på grund av symmetri och att x≥0 i området att den sökta integralen är
2 * INT_{y=0}^1 INT_{z=0}^{2-2y^2} INT_{0}^{2-z} x dx dz dy
där undre gränsen för y = 0 istället för -1.
Körde det i en 3d-grafritare nu och och om jag ser rätt så borde gränsen för y gå från -1 till 1? 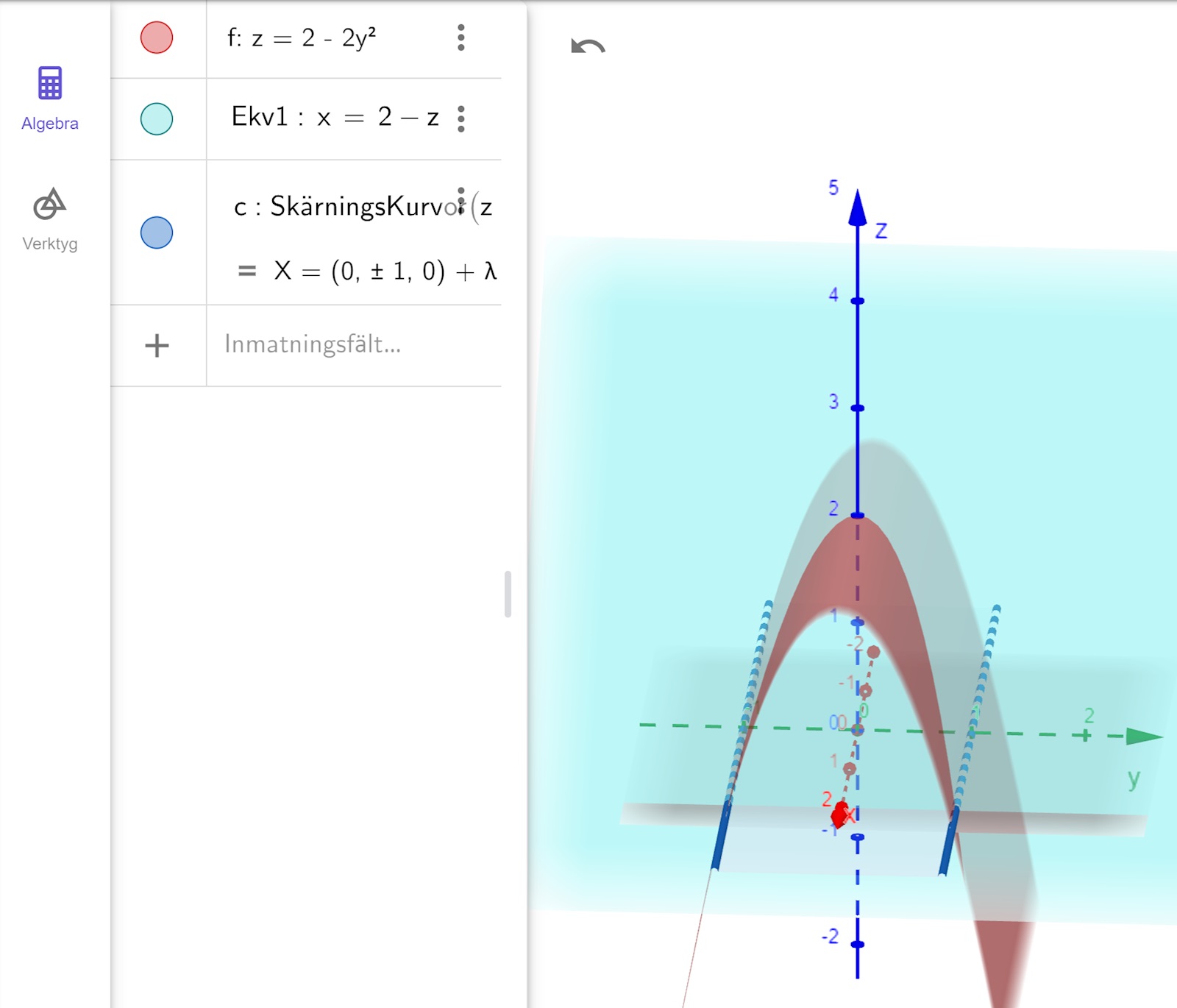
Yes jag klarar det nog härifrån Trinity2. Tack!
Haraldo skrev:Yes jag klarar det nog härifrån Trinity2. Tack!
Perfekt!
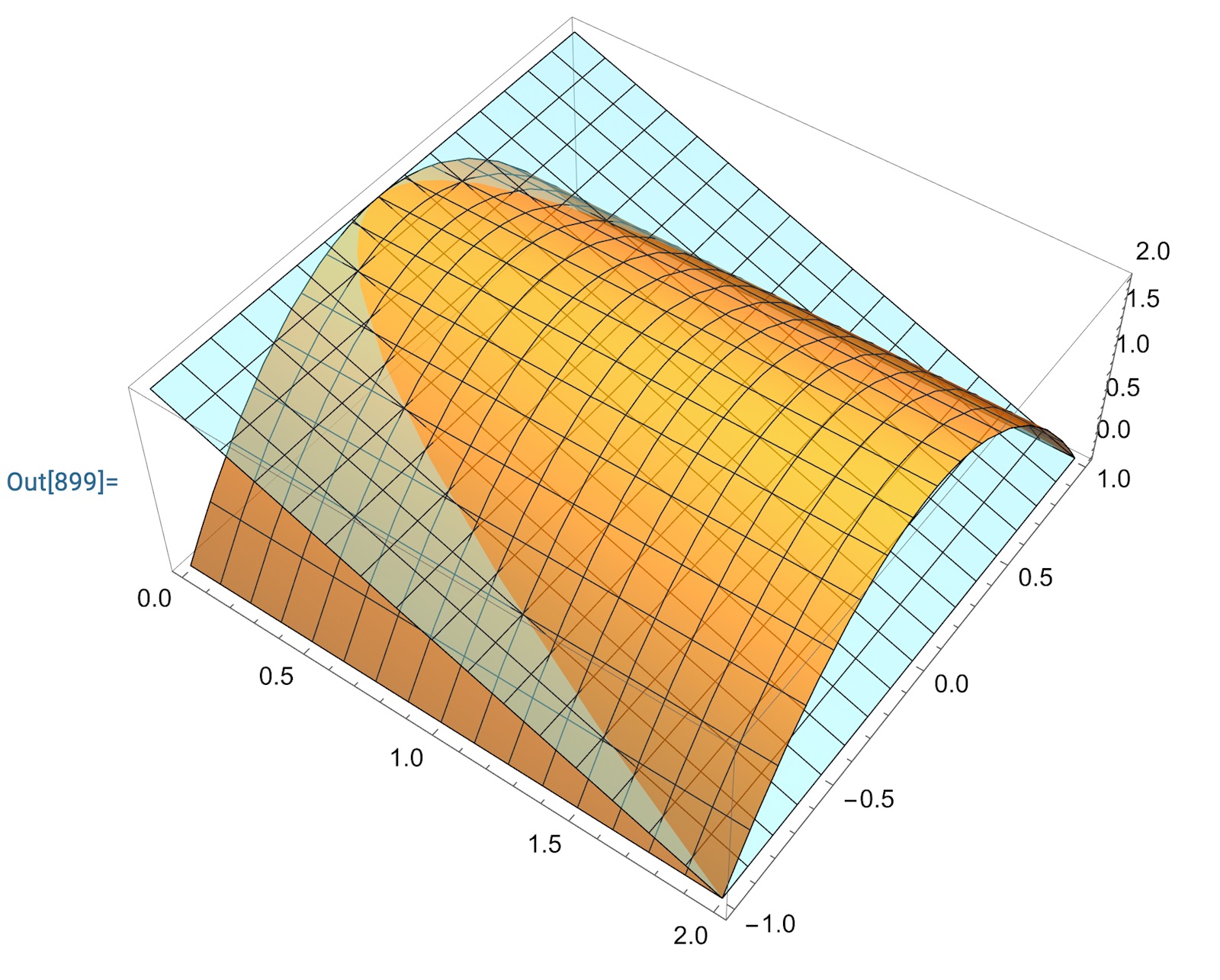
Här har du en liten bild på området