flervariabelanalys - största och minsta värde

$f(x,y)$ innehåller inga konstanttermer, det ska därför inte gå att få någon extra konstantterm när man sätter in $y=2x$

$f(x,2x)=x^2+2x\cdot(2x)-5\cdot (2x)^2=-15x^2$

Och detta ska enligt uppgiften vara lika med $10$.

Jag får om jag stoppar in f($\frac{y}{2}$,y) = $\frac{-15y^2}{4}$=$\frac{40}{4}$som blir -15y^2 = 40 väl? 

Ja, det stämmer, men i lösningen har de använt $y=2x$. Följande uttryck är då helt ekvivalenta:

$-15x^2=10$

$-15y^2=40$

Du skrev dock $-15x^2=40$ och det är omöjligt.

OK men jag fattar inte riktigt hur man inte vet hur det inte existerar ett största värde men det finns ett minsta av att veta f(3,1)=f(-3,-1)=5. Hur vet man att det är minsta värdet och inte största? 

Villkoret $f(x,y)=10$ är uppfyllt för obegränsat stora y.

Funktionen $g(x,y)$ kan därmed hämta obegränsat stora värden på $y$ från villkoret $f(x,y)=10$ och bli hur stor som helst.

Däremot kan $g(x,y)$ inte bli hur liten som helst eftersom vi vet att $g(x,y)=(x-y)^2+y^2\geq 0$ (summan av två kvadrater måste vara större än eller lika med noll). Dessutom saknar funktionen singulära punkter.

Därför måste eventuella extremvärden, om de existerar, vara minimipunkter. Men om man är osäker på vad man hittat kan man alltid göra en lokal undersökning av extremvärdet. Till exempel genom en Taylorutveckling runt punkten.

Jag fattar inte riktigt detta. Vad betyder "villkoret f(x,y) = 10 är uppfyllt för obegränsat stora y", varför ska man veta det? Varför ska man kolla det? Hur vet man det? Ska man göra samma sak för g(x,y) i a) delen också? Vad betyder det att funktionen saknar singulära punkter? Jag tog det som att det fanns ett likamed tecken och då saknas dem för att de inte ingår i funktionen?

Dessutom fattar jag inte varför i a) ellips innebär att det har ett största och minsta värde? Är det bara att den är kompakt? Och varför skrev de om den till (x-y)^2+y^2 = 10, ska man alltid göra det?

Ja, du har förstått det korrekt, i uppgift a) söker man extrempunkter på den kompakta mängden av en ellips. Eftersom mängden är kompakt vet vi garanterat att det finns ett största och ett minsta värde enligt en sats som jag tror att ni har bevisat!

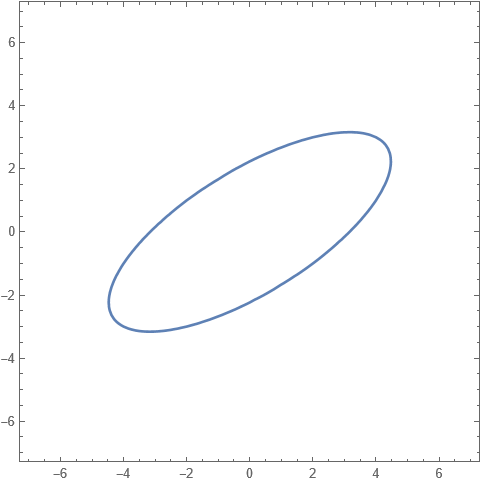
Men på uppgift b) söker vi värden på en hyperbel (den har två grenar). Och det visar sig att den mängden (kurvorna) varken är begränsad eller sluten

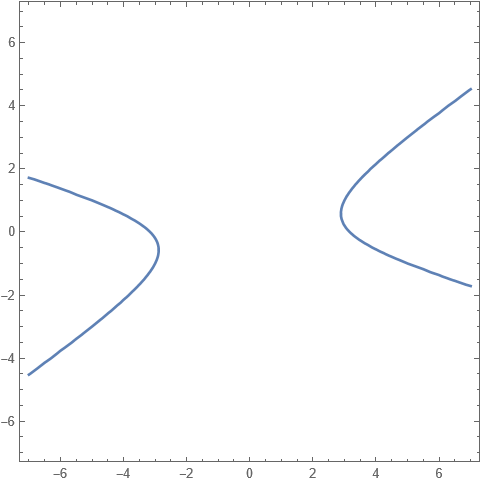Nu kan vi alltså inte längre garantera ett största och minsta värde. För att på ett enkelt vis visa att $g(x,y)$ kan anta godtyckligt stora värden väljer man att visa att den består av summan av två positiva kvadrater $g(x,y)=(x-y)^2+y^2$. Eftersom vi får hämta godtyckligt stora värden på $y$ (och därmed implicit $x=-y\pm \sqrt{10+6y^2}$) kan vi få $g(x,y)$ att anta hur stora värden som helst på stora avstånd från Origo. Funktionen saknar alltså ett största värde på hyperbelmängden. Däremot finns ett minsta värde i närheten av origo. Summan av två kvadrater måste ju vara $\geq 0$.

Finns ett minsta värde måste åtminstone Lagrangevillkoret vara uppfyllt där. Och det måste antas på ett begränsat avstånd från origo. Om du vill kan du se det som att du gör en avskärmning av hyperbeln runt origo och på så sätt skapar en kompakt mängd som du kan undersöka.

Jag fattar inte varför man gör två positiva kvadrater? Hur visar det att det kan anta stora värden och hur det saknar ett största värde? Jag fattar inte den delen

Funktionen $g(x,y)=(x-y)^2+y^2$ består av två kvadrater, båda större än noll. Därför kan man till exempel enkelt inse att

$y^2\leq (x-y)^2+y^2$

Vidare ger villkoret $f(x,y)=10$ inget krav på $y$, det får vara hur stort eller litet som helst. Vi kan låta det vara talet $m$

Då gäller alltså att $m^2\leq g(x,y)$

Eftersom vi får göra talet $m^2$ hur stort som helst och $g(x,y)$ är lika med eller ännu större måste vi dra slutsatsen att $g(x,y)$ kan bli oändligt stor. Ett största värde saknas. Vi kan också dra slutsatsen att $0\leq g(x,y)$.

Om vi däremot studerar funktionen $h(x,y)=x-y$ som inte består av kvadrater kan vi inte lika enkelt säga något om funktionen. T.ex. är $h(x,y)=0$ för alla $x,y$ under villkoret $x=y$, trots att $x,y$ får bli hur stora som helst. Det beror på att vi nu kan tal med olika tecken som tar ut varandra.

Det är inget magiskt med "kvadraten" och det är bara ett i raden av knep man kan använda för att uttala sig om hur små eller stora värden en funktion kan anta.

Hur blir det så? Om man utvecklar kvadraten blir det ju x^2 + 2xy +y^2 -6y^2 = 10 så varför försvinner (y^2) när de beräknar x ? 

Jag fattar fortfarande inte varför g(x,y) kan bli oändligt stort

x² + 2xy +y² -6y² = 10

(x² + 2xy +y²) -6y² = 10 Använd kvadreringsregeln baklänges på uttrycket i parentesen

(x+y)² - 6y² = 10 så ser man att det är en ellips, men vriden

Hur vet man att g är oändligt stort?

i a) undersöker vi g och ser att det är en ellips och då antar f därmed ett största o minsta värde men i b) ser vi att det är en ellips men den är vriden (hur vet man det bara från ekvationen?) och då kan g inte (antingen) anta ett största eller minsta värde? hur vet man vilket det är dvs att det är oändligt stort eller oändligt litet?

$g(x,y)=10$ är en ellips

$f(x,y)=10$ är en hyperbel.

Se bilderna ovan. Ekvationen $f(x,y)=10$ kan skrivas om på följande vis

$x^2+2xy-5y^2=10$

$(x+y)^2-6y^2=10$

$(x+y)^2=10+6y^2$

$(x+y)=\pm\sqrt{10+6y^2}$

$x=-y\pm \sqrt{10+6y^2}$

Nu kan vi om vi vill sätta in godtyckligt stora värden på $y$ och ändå räkna ut en punkt $(x,y)$ som hamnar på hyperbeln

Låt till exempel $y=100$, då är $x=-100+\sqrt{10+6(100)^2}\approx 145$

Låt till exempel $y=10^5$, då är $x=-10^5+\sqrt{10+6\cdot 10^{10}}\approx 150000$

Att $y$ kan anta godtyckligt stora värden innebär i sin tur att eftersom $y^2\leq g(x,y)$ kan $g(x,y)$ bli hur stort som helst.