Flervariabelanalys, polära koordinater i trippelintegral

Du bör definitivt rita upp en bild ja. När jag läste flervariabeln var konen också spännande at first. Men ritar du kanske du kan se varför?

förstår inte riktigt hur jag ritar konen är det z = (x^2+y^2)^1/2?

Ja, det är konen. Se vad som händer om du låter x respektive y vara noll. Då ser du hur ytan skär yz-planet och xz-planet. Då ser du hur konen kommer se ut. 

Detta är utan den andra sfäriska ytan blev krånligt o rita, men vet hur den ser ut.

Stämmer detta för konen och dess bidragen till området K?

Så här. Olikheterna i uppgiften ger att området är under konen, men begränsas av att det ligger inuti enhetsklotet. 

Men borde i theta då variera mellan 45 grader och -45 grader från z-axeln dvs från 45 grader till 315 grader??

Gränserna ser konstiga ut i lösningsförslaget, nästan lika konstiga som ordet "en sfärer" i uppgiften. Den vinkel som inte är från 0 till $2\mathrm{\pi }$ ser ut att vara från $-\frac{\mathrm{\pi }}{4}$till $\frac{\mathrm{\pi }}{4}$.

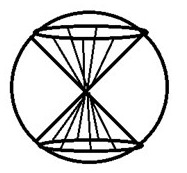
Ytan är ju z=rotenur något, alltså z kan inte vara negativt. Ytan är bara den övre konen, och nedåt begränsas kroppen av sfären. 

Så jag tycker lösningsförslagets gränser stämmer. 

Då bör det väl vara den vita delen? Skall inte "den andra vinkeln" ligga mellan 0 och pi/4 i så fall?

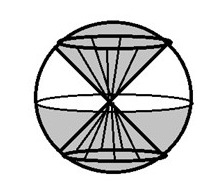
Nej, det tycker jag inte. Trippelintegralen är över en kropp K. 

K ligger inuti enhetssfären. K är dessutom begränsad uppåt av ytan z=sqrt(x^2+y^2)

Edit: K är alltså enhetsklotet med en kon borttagen från toppen så att säga.

Edit2: Med sfäriska koordinater räknas den vinkeln från positiva z-axeln, så intervallet pi/4 till pi stämmer. 

Den här då? Det vita, alltså.

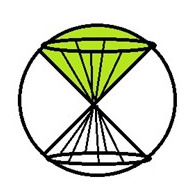
Det ser bra ut. 

Det är bara att konstatera: Läsförståelse ÄR svårt.