Flervariabelanalys - Kvadratiska formen med tre variabler
Längst ner är frågan och facit. Jag förstår, och har räknat, allt fram till termen 4hl i Q(h,k,l) ekvationen.
I vanliga fall (med två variabler) så är formeln: f``xx(x,y)h^2 + f´ýy(x,y)k^2 + f``xy(x,y)*2
och jag kan se att de andraderivatorna från respektive variabel (x,y,z) även förekommer i ekv nedan för fallet med tre variabler, den jag inte lyckas räkna ut är vad motsvarigheten till termen f``xy(x,y)*2 är i denna ekvation och hur den blir 4hl.
Jag har räknat ut alla andraderivator enligt:
f``xy = 4xy = f``yx
f``xz = 2 = f``zx
f``yx = 0 = f``zy
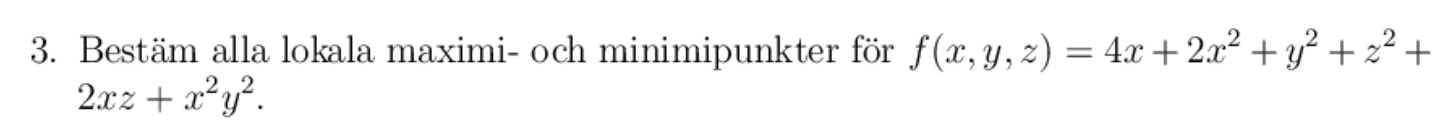

Jag minns inte flervariabelanalysen speciellt bra, men det borde väl gå att projicera på xy-, yz- och zx-planen, räkna tvådimensionellt och sedan summera alltihop?
Någon som har bättre minne kommer säkert att korrigera mig, hoppas jag.
Du har räknat ut 3 av andraderivatorna. De övriga är f"xx =4+2y2, f"yy = 2+2x2 och f"zz = 2 (kontrollera!)
Uttrycket för andraderivatan i tre dimensioner i en punkt x,y,z är
Notera kvadraten som kommer från Taylors formel (ur andraderivatan)
Utvecklar du detta med hjälp av derivatorna ovan har du
f"xx(-2,0,2)h2 + f"yy(-2,0,2)k2 + f"zz(-2,0,2)l2 + 2f"xy(-2,0,2)hk+2f"xz(-2,0,2)hl + 2f"yz(-2,0,2) =
4h2+ 10k2+2l2 + 0 + 4hl + 0
och därefter löser du det med ovanstående resonemang.

