Flervariabelanalys: kallas tangentplan för tangentkuber eller nåt annat i högre dimensioner än 3? (Matematik/Universitet)

Generellt kan man kalla tangentlinjer, tangentplan o.s.v. för tangentrum.

Jag tror inte man har någon specifik term för ett tangentrum av dimension tre (tangentvolym kanske skulle passa?), utan att man istället använder det mer generella ordet tangentrum.

En intressant fråga att ställa är vad ett tangentrum till en trevariabelfunktion ens är.

!

Vilket fint ord, och vad det passar!

AlvinB skrev:
En intressant fråga att ställa är vad ett tangentrum till en trevariabelfunktion ens är.

Ja... Samma betydelse som tangentplan men en dimension till, jag vet inte vad det säger mig.

Qetsiyah skrev:
!
Vilket fint ord, och vad det passar!
AlvinB skrev:
En intressant fråga att ställa är vad ett tangentrum till en trevariabelfunktion ens är.
Ja... Samma betydelse som tangentplan men en dimension till, jag vet inte vad det säger mig.

Till att börja med behöver vi ju reda ut att för att kunna betrakta ett tangentrum behöver vi ju arbeta i ett rum med en dimension till utöver tangentrummets dimension.

För en tangentlinje (dimension 1) behöver vi betrakta kurvan i ett tvådimensionellt plan för att få något geometriskt grepp om saken.

För ett tangentplan (dimension 2) behöver vi betrakta ytan i en tredimensionell rymd för att få någon geometrisk förståelse.

För ett tangentrum i dimension 3 borde vi då rimligen behöva betrakta volymen i ett fyrdimensionellt rum för att kunna göra något liknande. På samma sätt som ett tangentplan i ett tredimensionellt vektorrum beskrivs av en ekvation $ax_1+bx_2+cx_3+d=0$ borde vi då kunna beskriva ett tredimensionellt tangentrum i ett fyrdimensionellt vektorrum med en ekvation $ax_1+bx_2+cx_3+dx_4+e=0$ .

Vi kan då tänka oss att eftersom en normalvektor till tangentrummet för en funktion $f$ i en dimension betraktat i ett tvådimensionellt plan ges av:

$(\dfrac{\partial f}{\partial x_1},-1)$

och i två dimensioner betraktat i ett tredimensionellt rum av:

$(\dfrac{\partial f}{\partial x_1},\dfrac{\partial f}{\partial x_2},-1)$

borde man väl rimligen kunna hävda att ett tangentrum till en tredimensionell volym betraktat i ett fyrdimensionellt rum har normalvektorn

$(\dfrac{\partial f}{\partial x_1},\dfrac{\partial f}{\partial x_2},\dfrac{\partial f}{\partial x_3},-1)$

Det där låter inte så rigoröst, men väldigt övertygande ändå.

Det var lite just det som jag ville belysa. Det är inte helt självklart vad ett tangentrum i dessa högre dimensioner ens är. Det jag skrev ovan är en möjlig tolkning.

Det finns en lite mer rigorös definition inom differentialgeometrin, men jag kan inte påstå att jag är särskilt bekant med den.

Det där ska jag se närmre på

Den huvudsakliga frågan har jag nog inget svar på (mer än "3-dimensionellt tangentrum"), men AlvinB lyfter lite intressanta funderingar som jag tänker kan vara kul att säga något om.

Vad är den högre-dimensionella analogen till kurvor och ytor?

Kurvor och ytor kan absolut generaliseras till högre dimensioner, till något som kallas för mångfalder. Väldigt förenklat uttryckt är en $m$ -dimensionell mångfald ett geometriskt objekt som vid varje punkt ser ut som en bit av $\mathbb{R}^m$ , om man zoomar in tillräckligt mycket.

Lite mer precist är det ett topologiskt rum (med detta menar vi en mängd punkter där det är meningsfullt att tala om omgivningar av punkterna), sådant att man lokalt vid varje punkt kan tänka sig en $m$ -dimensionell parametrisering av rummet [eller ekvivalent: kan införa ett lokalt $m$ -dimensionellt koordinatsystem]. Dessutom vill man att de här lokala parametriseringarska vara kompatibla med varandra, i bemärkelsen att om två lokala parametriseringar överlappar med varandra, så kan man byta från den ena parametriseringen till den andra med en oändligt deriverbar funktion.

Kurvor (t.ex. en helix eller en cirkel) är med den här definitionen på 1-dimensionella mångfalder, och ytor (t.ex. en sfär eller torus) är 2-dimensionella mångfalder.

Här en bild från ett arbete jag skrev för några år sedan, som är tänkt att illustrera hur en sådan här lokal parametrisering/lokalt koordinatsystem skulle kunna se ut (i fallet $m=2$ ):

Har de här högre-dimensionella objekten en analog till tangentlinjer och tangentplan?

Om vi låter $M$ vara en $m$ -dimensionell mångfald, och $p\in M$ vara en punkt på $M$ , så kan vi definiera tangentrummet $T_pM$ vid punkten $p$ . Detta kommer vara ett $m$ -dimensionellt vektorrum. Exakt hur man definierar det här vektorrummet är lite klurigt. Eller ja, det beror på. Om vår mångfald $M$ ligger inbäddad i $\mathbb{R}^n$ för något $n$ (som måste vara minst lika stort som $m$ , precis som redan har påpekats här i tråden), så är det inte så svårt, utan då kan vi helt enkelt säga att $T_pM$ består av alla derivator som en kurva i mångfalden som paserar punkten $p$ kan ha, just när de passerar punkten $p$ . Mer precist:

$T_pM=\{{\gamma'(0)}:\begin{matrix}\gamma:(-1,1)\to M\\\text{is a curve with $\gamma(0)=p$}\end{matrix}\}\,.$

Bild från Wikipedia som illustrerar detta ganska bra:

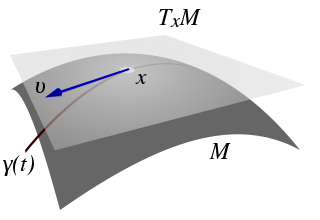
Detta gissar jag är mer eller mindre exakt hur du är van vid att definiera tangentlinjer och tangentplan för kurvor och ytor, så det är en ganska naturlig generalisering att göra. Och tack varje Whitneys så kallade inbäddningssats, så vet vi att varje mångfald kan betraktas som inbäddad i $\mathbb{R}^n$ om vi bara väljer $n$ tillräckligt stort (men man behöver aldrig gå högre än $n=2m$ ), så i någon mening behöver vi egentligen inte krånlga till det mer än så här.

I praktiken vill vi dock gärna krånlga till det lite till! :D

Bland annat efter som det finns gott om exempel på mångfalder där det inte alls är speciellt självklart hur man ska bädda in $\mathbb{R}^n$ för något $n$ . Den berömda Kleinflaskan är ett exempel på detta. Det är en 2-dimensionell mångfald som inte går att bädda in i 3D, utan om vi vill bädda in den någonstans så behöver vi minst 4D, och det finns inget helt snyggt sätt att göra det, så vitt jag känner till, utan det blir ganska kladdigt. För att slippa hålla på och kladda med de här inbäddningarna, som ofta inte riktigt fångar mångfaldens fundamentala egenskaper så sngygt, så har man därför utvecklat en så kallad intrinsic (oklart vad man ska säga på svenska) definition av tangentrummet, som bara är baserad på vad som sker inne i själva mångfalden, och som inte kräver att man tittar på den "utifrån" från något större omgivande rum. Detta har visat sig vara ett oerhört kraftfullt perspektiv, och det är ofta det man använder när man studerar mångfalder i modern matematik.

Exakt hur den här "instrinsic" definitionen fungerar är lite komplicerat. Förenklat kan man säga att man först bildar mängden $C^\infty(M)$ av alla oändligt deriverbara funktioner $M\to\mathbb{R}$ på mångfalden $M$ [man kan tänka sig alla funktioner som kan användas för att mäta någon slags storhet som typ "temperatur" på mångfalden], och sedan låter $T_pM$ vara mängden av alla tänkbara operatorer på $C^\infty$ som beter sig som "riktningsderivator" i punkten $p$ (mer precist vill man att de vara linjära och uppfylla produktregeln). Notera att den första definitionen kräver att det finns ett omgivande rum (annars makear $\gamma'(0)$ inte sense), medan den här mer abstrakta definitionen inte kräver det.

Anledningen till att detta är en rimlig generalisering är att för inbäddade mångfalder så finns det en naturligt 1-till-1-förhållande mellan det konkreta och det abstrakta tangetrummet: varje tangentvektor motsvarar en riktningderivata i just den riktningen (och vice versa).

Sorry om det här inte makear så mycket sense. Fråga gärna om du vill att jag eller någon annan ska försöka förklara det här lite bättre och mer ingående, men poängen är att det finns en väl utvecklad teori för högre-dimensionella objekt. Om man vill lära dig mer om detta så är boken Introduction to Smooth Manifolds av John Lee hyfsat lättillgänglig, och i princip skulle man skulle kunna testa att bläddra lite i den redan när man är klar med flervariabel-kursen (även om man nog borde läsa en kurs i differentialgeometri för kurvor och ytor innan man på allvar ger dig i kast med att läsa om högre-dimensionella mångfalder).

Bonusfråga: Varför bryr man sig om högre-dimensionella mångfalder och deras tangentrum?

De dyker upp överallt i matematiken! Ett snabbt exempel handlar om symmetri och differentialekvationer. Jag som tycker kemi och sånt är kul är till exempel ibland intresserad av Schrödinger-ekvationen, och för att lösa den behöver man ofta utnyttja att ens system på ett eller anant sätt är symmetriskt. För väteatomen, som är det mest grundläggande fallet i kemin, så har vi till exempel rotationssystmetri, och då vet vi att mängden av alla rotationer i 3D, alltså

$\mathrm{SO}(3)=\{A\in\mathbb{R}^{3\times 3}:A^TA=I\:\:\text{och}\:\:\det(A)=1\}$

kommer att "verka" på vektorrummet av alla lösningar som vi förväntar oss att få fram. Exakt hur den här verkan går till är svårt att förstå, men något som hjälper väldigt mycket på vägen, är att $\mathrm{SO}(3)$ visar sig vara en 3-dimensionell mångfald, och därför har ett 3-dimensionellt tangentrum, som vi kan förstå väldigt väl med hjälp av linjär algebra. Och på ett nästan magiskt sätt (som är en del av det man kallar för Lie-teori) så kan kunskapen om tangentrummet användas för att förstå $\mathrm{SO}(3)$ , vilket i sin tur kan användas för att förstå lösningarna till Schrödinger-ekvationen för väte.

Det här säger ju så klart inte så mycket om man inte vet vad jag pratar om, och detaljerna kräver ganska mycket förkunskaper (eller att man är bättre på att förklara än jag är), men poängen är mest att försöka ge en liten känsla för hur mångfalder och tangentrum kan dyka upp i ett sammanhang där det inte vid första anblick är väntat att de ska dyka upp. Vill man lära sig mer om detta är gruppteori, representationsteori och Lie-teori nyckelord att hålla utkik efter när man bläddrar i böcker eller funderar på framtida kursval!

Nu kommer jag tillbaka till tråden!

I samband med min undersökning om tensorer kom jag in på multilinjär algebra och tensoranalys, vääääääälidgt intressant. Mitt mål är att förstå mig på Stokes generaliserade sats (på riktigt) nån gång.

Eftersom jag frågade det här innan jag hade pluggat linjär algebra och flervariabelanalys (och saknade en hel del matematisk mognad och exponering) så förstod jag inte mycket utom bilden du la upp.

I alla fall, det där med intrinsic och extrinsic derivator kom jag i kontakt med när jag undersökte tensorer, det makade mycket intuitive sense.

$\text{SO(3)}$ Har jag väl stött på angående rotationssymmetrier på kuben? De två kraven om ortogonalitet och ett determinant är samma. Jag har en fråga här, varför säger man att gruppen verkar på $\mathbb{R}^3$ när det egentligen är matriserna som gör det? När du definierar gruppen sådär, är det underförstått att additionsoperationen är multiplikation mellan matriser?

Har du något tips på bok om tensoranalys, men med nära koppling till differentialgeometri?