Flervariabel, stationära punkter av (x,y)funktion
Hej, har fått en uppgrif som förljer:
Betrakta funktionen f(x,y)=(2x-y)^2 (x-4) Finn alla stationära punkter.
Jag har tagit de partiella derivatorna och fick f'x=(2x-y)(6x-16-y) och f'y=-2(2x-y)(x-4)
När jag ska hitta x och y värden för 0 ställen hittar jag att det händer när något av dessa fall följer:
0=2x-y , 0=6x-16-y , och när x=4.
Men jag är förvirad med vad denna informationen sägger. Jag antar att funktionen har en linje enligt y=2x, där alla värden är stationära punkter, men hur förklarar man det på ett bra sätt. Eller missade jag något. Jag försökte byta in y=2x i 0=6x-16-y och få 0=4x-16 och där får jag också x=4. är (4,8) någon speciel punkt? för den får sama värde i funktionen som (5,10)
Tack i förväg
Germantas skrev:Hej, har fått en uppgrif som förljer:
Betrakta funktionen f(x,y)=(2x-y)^2 (x-4) Finn alla stationära punkter.Jag har tagit de partiella derivatorna och fick f'x=(2x-y)(6x-16-y) och f'y=-2(2x-y)(x-4)
När jag ska hitta x och y värden för 0 ställen hittar jag att det händer när något av dessa fall följer:
0=2x-y , 0=6x-16-y , och när x=4.Men jag är förvirad med vad denna informationen sägger. Jag antar att funktionen har en linje enligt y=2x, där alla värden är stationära punkter, men hur förklarar man det på ett bra sätt. Eller missade jag något. Jag försökte byta in y=2x i 0=6x-16-y och få 0=4x-16 och där får jag också x=4. är (4,8) någon speciel punkt? för den får sama värde i funktionen som (5,10)
Tack i förväg
Välkommen till Pluggakuten!
Nu har du hittat att f'x = 0 om y = 2x eller om y = 16-6x och att f'y = 0 om y = 2x eller om x = 4. Kan du hitta några punkter där båda derivatorna har värdet 0?
Här är en plot från WolframAlpha
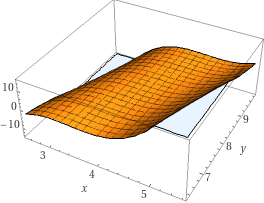
ja, jag har ju speciellt punkten (4,8) som löser alla dessa, men på båda partiella derivatorna kan alla x värden fungera sålänge y värdet är 2x. Innebär det att det finns oändligt med punkter? eller missar jag något?


