Flervariabel - rotationssymmetrisk kropp

ipsum skrev:

• Finner det underligt var (-y)^2 kom ifrån i mellanledet? I det nya koordinatsystemet är väl x->y och y->-x, så ska det inte stå antingen (y)^2 eller (-x)^2 i mellanledet, beroende på vilken koordinat de konverterade till den nya koordinaten. Men det känns logiskt att de försökt konvertera x koordinaten till den nya koordinaten, vilket borde egentligen ge y och inte -y?

Jag förstår inte heller varför de har minustecken. De verkar ha gjort en 90-gradig negativ transformation istället. Det förändrar inte resultatet som blir uppenbart om man ritar för hand eller i graf:

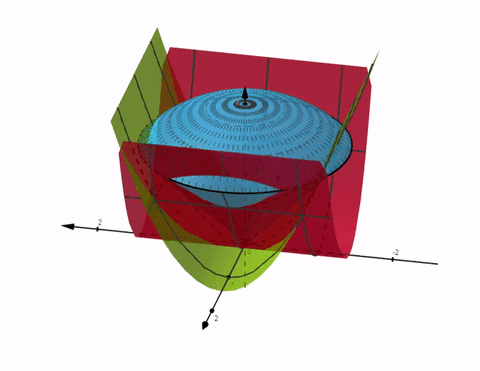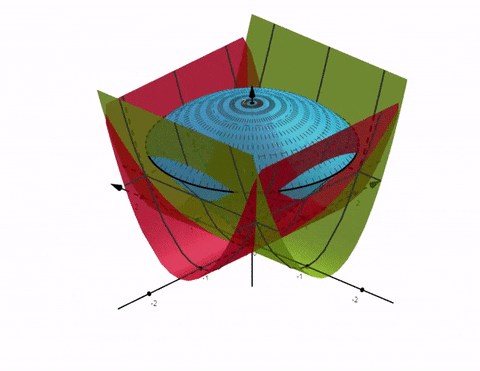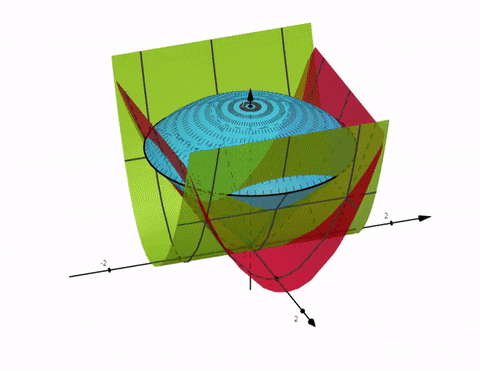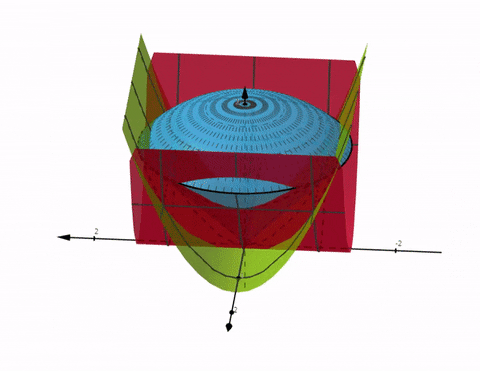
Grön är alltså $z = x^2$, röd är $z=y^2$ och blå är ytan som omsluter området $K$.

• Dessutom i sista ledet verkar de konvertera tillbaka koordinaten till originella koordinatsystemet, men då är väl integranden bara lika med x^2, man går liksom bara fram o tillbaka?

Ja, precis. Det är poängen. Du skulle kunna jobba med dummy-variabler så som u, v, w och sedan byta tillbaka men det är överflödigt. I transformationen så är x-axeln parallell med ursprungliga y-axeln. Med rotationssymmetri hos området ($T{K}=K$) får du resultatet.

• Hur vet man att K är rotationssymmetrisk? 

Det är en kon med ett sfäriskt segment som lock. Du kan rita och se att det är rotationssymmetriskt kring z-axeln. 

• Vad för konsekvenser fås av att jakobian determinanten är exakt 1? Att den är nollskild innebär bara att vi har en bijektiv avbildning, men exakt 1 kanske innebär att egenskaper hos integranden då bibehålls, t.ex att y och x är udda, vilket kommer vara fallet efter variabelbytet också?

Det betyder att koordinatbytet inte sträcker på axlarna något. Jämför med från kartesiska till polära där du har:

$dxdy = rdrd\theta$ 

Här skalar alltså faktorn $r$ om areaelementet (sträcker och skjuvar symmetriskt). Denna faktor kommer från Jakobianen.