Flervariabel - normal till Flödesintegral

Har en undring gällande fråga a). Jag läste av normalvektorn n till ytan s med ögonmått genom att inse att det borde vara ortsvektorn till en godtycklig punkt på kvartscirkeln, men eftersom vi söker en normalvektor så måste man normalisera ortsvektorn med längden av vektorn, vilket är just radien av kvartscirkeln. Därmed fick jag
n=(0,y,z)r=(0,y,z)2.
När jag däremot kollar på facit får de fram att det är liknande förutom att dividera med 2, vilket jag inte förstår. Jag förstår att man kan komma fram till normalvektorn på annat sätt, genom att beräkna kryssprodukten av de partiella derivatorna av en parametrisering av ytan, och det hade jag kunnat göra, men det kändes mer lämpligt att bara använda ögonmått på detta då det var inte så svårt att avläsa den. Jag förstår dock inte varför mitt sätt att ta fram normalvektorn är felaktig?
Dessutom är jag lite förvirrad över deras beskrivning av orienteringen. De säger bort från x-axeln, så betyder det då att vi inte behöver beräkna flödet från botten- och toppenlocket eftersom flödena ut från dem är parallella med x-axeln, därmed efterfrågas endast flödet ut från mantelytan av cylinderstycket?
Här är facit:
Jag har några tips:
- Bäst är alltid att lägga upp en bild på facit då din tolkning och parafrasering kan vara felaktig.
- Om lösningen gör något annat än du, fortsätt arbeta och se om du får rätt svar. Det kan helt enkelt vara så att de hoppar över några steg som gör det svårt att följa lösningen.
- Du har en korrekt normalvektor, den är inte felaktig. Tänk dock på vad infinitesimalen i flödesintegralen d→N beskriver när den (Edit: ytelementet) kombineras med normalvektorn.
- Det står explicit att du ska parametrisera ytan vilket du inte gjort när du beskrev normalvektorn. Jag förväntar mig något som:
→n=(0,ρcos(t),ρsin(t))
SaintVenant skrev:Jag har några tips:
- Bäst är alltid att lägga upp en bild på facit då din tolkning och parafrasering kan vara felaktig.
- Om lösningen gör något annat än du, fortsätt arbeta och se om du får rätt svar. Det kan helt enkelt vara så att de hoppar över några steg som gör det svårt att följa lösningen.
- Du har en korrekt normalvektor, den är inte felaktig. Tänk dock på vad infinitesimalen i flödesintegralen d→N beskriver när den är kombinerad med normalvektorn.
- Det står explicit att du ska parametrisera ytan vilket du inte gjort när du beskrev normalvektorn. Jag förväntar mig något som:
→n=(0,ρcos(t),ρsin(t))
Sant, borde ha nämnt utförligt hur jag gjort:
Normalvektorn får jag till efter insättning av parametriseringen
r(x,t)=(x,2cost,2sint) =>
(0,y,z)2={y=2cost,z=2sint}=(0,cost,sint)
Redan här ser jag att får en hälften så liten normalvektor, vilket reflekteras sedan i mitt svar, där jag får 12 istället för 24 som de fick i facit (kolla på facit jag lade upp ovan).
Jag har alltså samma uträkning som facit, förutom att normalen är hälften så stor, det är den enda skillnaden. Jag förstår inte din hint: "Tänk dock på vad infinitesimalen i flödesintegralen d→N beskriver när den är kombinerad med normalvektorn." Är det kanske därför jag i integranden inte får samma vektor för normalvektorn?
Ja, om du vill beskriva en enhetsvektor ˆn genom att dela med längden på ortsvektorn (radien ρ hos cylindern), försök då beskriva ytelementet dS. Detta blir enkelt för en cylinder:
dS=ρ
En flödesintegral i grundform beskrivs som:
Du ser alltså att längden på ortsvektorn dyker upp i ytelementet och flödesintegralens infinitesimala "ytnormalvektor" blir:
Detta är samma som lösningen i facit.
SaintVenant skrev:Ja, om du vill beskriva en enhetsvektor genom att dela med längden på ortsvektorn (radien hos cylindern), försök då beskriva ytelementet . Detta blir enkelt för en cylinder:
En flödesintegral i grundform beskrivs som:
Du ser alltså att längden på ortsvektorn dyker upp i ytelementet och flödesintegralens infinitesimala "ytnormalvektor" blir:
Detta är samma som lösningen i facit.
Ja, du har helt rätt, den lilla detaljen hade jag glömt! fås genom att multiplicera med normalvektorn av ortsvektorn, vilket alltså är ekvivalent med ortsvektorn utan normaliseringen.
Jag antar att detta är vad som händer när jag inte är ordentlig med definitionerna...
Tack för hjälpen!
Ytterligare en fråga:
"De säger bort från x-axeln, så betyder det då att vi inte behöver beräkna flödet från botten- och toppenlocket eftersom flödena ut från dem är parallella med x-axeln, därmed efterfrågas endast flödet ut från mantelytan av cylinderstycket?"
Hur tolkar man bort från x-axeln? Är det just eftersom om man betraktar flödet ut ur bottenlocket av kvartscirkeln och topplocket så är dem flödens parallella med x-axeln, vilket inte är bort från x-axeln, och därmed beaktas dessa inte alls?
Endast flödena som uppfyller kravet "bort från x-axeln" är flödens ut ur mantelytan av cylinderstycket?
ipsum skrev:Ytterligare en fråga:
"De säger bort från x-axeln, så betyder det då att vi inte behöver beräkna flödet från botten- och toppenlocket eftersom flödena ut från dem är parallella med x-axeln, därmed efterfrågas endast flödet ut från mantelytan av cylinderstycket?"
Det finns varken botten- eller ett toppenlock. Det är ett cylinderytstycke enligt figuren nedan:

Du tar skalärprodukt mellan vektorfältet och ytvektorn som löper normalt till ytan enligt animationen nedan:
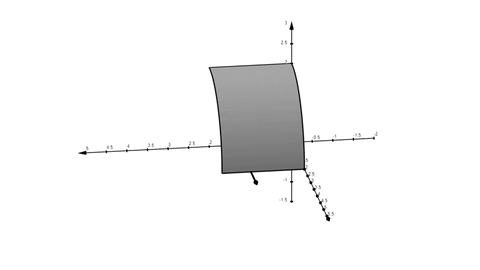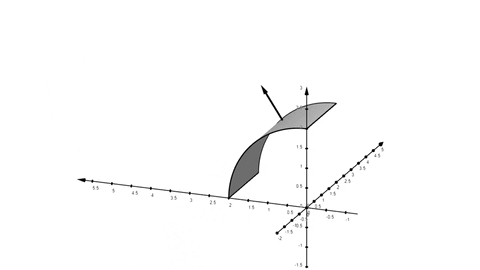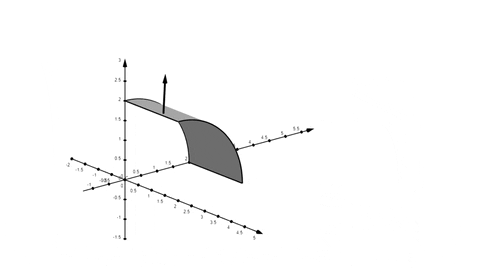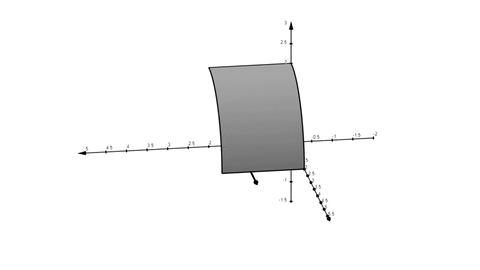
Totala bidraget av "projektionerna av vektorfältet i normalriktningen " blir totala flödet i riktning bort från x-axeln.
Tillägg: 30 maj 2022 17:41
Notis: Detta innebär att flödet ut genom ett botten- och toppenlock skulle vara lika med noll utifall att de beskrev ytan med dessa inkluderade. Detta därför att de är vinkelräta till x-axeln (bidrar ej till flödet i vad som blir radiell riktning i cylindriska koordinater).
SaintVenant skrev:ipsum skrev:Ytterligare en fråga:
"De säger bort från x-axeln, så betyder det då att vi inte behöver beräkna flödet från botten- och toppenlocket eftersom flödena ut från dem är parallella med x-axeln, därmed efterfrågas endast flödet ut från mantelytan av cylinderstycket?"Det finns varken botten- eller ett toppenlock. Det är ett cylinderytstycke enligt figuren nedan:
Du tar skalärprodukt mellan vektorfältet och ytvektorn som löper normalt till ytan enligt animationen nedan:
Totala bidraget av "projektionerna av vektorfältet i normalriktningen " blir totala flödet i riktning bort från x-axeln.
Tillägg: 30 maj 2022 17:41
Notis: Detta innebär att flödet ut genom ett botten- och toppenlock skulle vara lika med noll utifall att de beskrev ytan med dessa inkluderade. Detta därför att de är vinkelräta till x-axeln (bidrar ej till flödet i vad som blir radiell riktning i cylindriska koordinater).
Fin bild! Vilket program användes för att skissa detta?
För övrigt tror jag att jag fattar var min felaktiga uppfattning av ytan kom ifrån. Jag måste ha tolkat ekvationen som
vilket det såklart inte är. Men om den såg ut sådär då hade det funnits något "lock" på yz-planet då x=0 av cylindern och på x=2 måste jag anta. Men som sagt så var ekvationen annorlunda, så därför ser det ut såsom på bilden du visade.
ipsum skrev:Fin bild! Vilket program användes för att skissa detta?
Geogebra 3D
För övrigt tror jag att jag fattar var min felaktiga uppfattning av ytan kom ifrån. Jag måste ha tolkat ekvationen som
vilket det såklart inte är. Men om den såg ut sådär då hade det funnits något "lock" på yz-planet då x=0 av cylindern och på x=2 måste jag anta. Men som sagt så var ekvationen annorlunda, så därför ser det ut såsom på bilden du visade.
Glädjande att det löste sig och klarnade kring var du tänkt fel men rätt.


