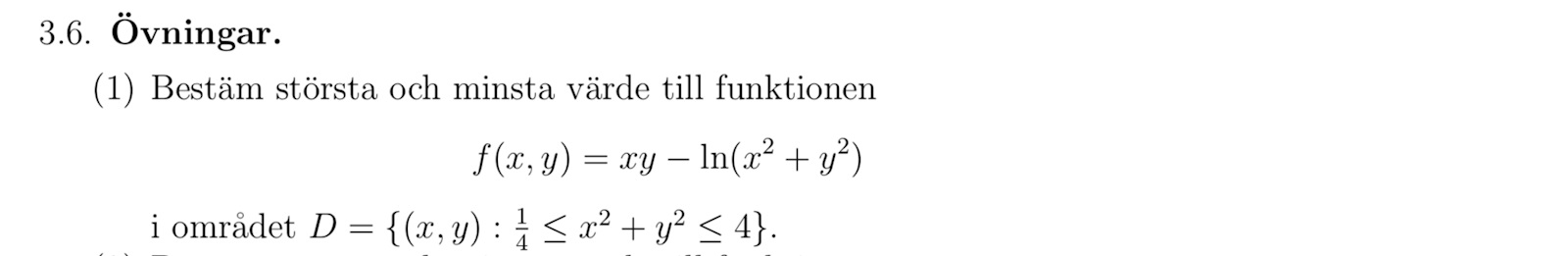FlerVar 3.6.1
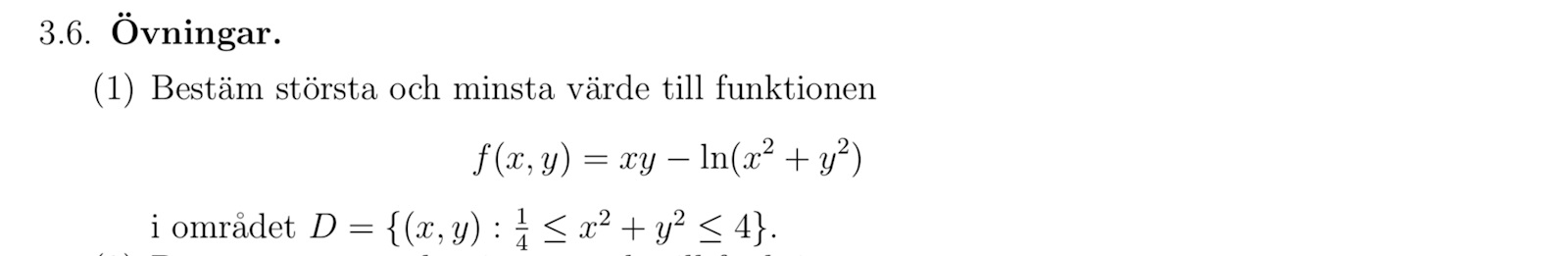
Jag får minsta värdet till 1-ln2 och största värdet till 2-2ln2. Rätt svar är -2-2ln2 och 1/8 +2ln2.
Till att börja med så ser jag att f(x,y)=f(y,x). Därför tänker jag att funktionen är symmetrisk med avseeende på x och y. Vilket gör att jag kan ”spegla” de punkter jag hittar.
fx’ har jag skriver i grön och fy’ skriver i rött. Därefter jag den första minus den andra och får att x=y. Antar att jag skulle kunna dra den slutsatsen direkt i och med att funktionen är symmetrisk med avseende x och y. Använder x=y till första och får x=y=1=-1 till lösning vilket ger punkterna, (1,1) och (-1,-1). Tror jag har gjort rätt hittills.
Sedan återstår att undersöka randpunkterna. Då jag har (1/2)^2 <=x^2 +y^2 <= (2^2) så tolkar jag det som att jag har två ringar att undersöka en ring med radie 1/2 och en med radie 2, med mittpunkter i origo.
Det gör att jag kan kallas x=2cost och y=2sint för den större och x=(1/2)*cost och y=(1/2)sint.
Sätter in h(2cost,2sint)= 2*2*cost*sint- ln1= 2*sin2t
h’t=4cos(2t)=0. Vilket ger mig t=pi/4 och 3pi/4, se uträkning nedan. Gör motsvarade för den lilla ringen. Vart någonstans är det jag gör fel?
Tack!

Philip22 skrev:
Jag får minsta värdet till 1-ln2 och största värdet till 2-2ln2. Rätt svar är -2-2ln2 och 1/8 +2ln2.
Till att börja med så ser jag att f(x,y)=f(y,x). Därför tänker jag att funktionen är symmetrisk med avseeende på x och y. Vilket gör att jag kan ”spegla” de punkter jag hittar.
fx’ har jag skriver i grön och fy’ skriver i rött. Därefter jag den första minus den andra och får att x=y. Antar att jag skulle kunna dra den slutsatsen direkt i och med att funktionen är symmetrisk med avseende x och y. Använder x=y till första och får x=y=1=-1 till lösning vilket ger punkterna, (1,1) och (-1,-1). Tror jag har gjort rätt hittills.
Sedan återstår att undersöka randpunkterna. Då jag har (1/2)^2 <=x^2 +y^2 <= (2^2) så tolkar jag det som att jag har två ringar att undersöka en ring med radie 1/2 och en med radie 2, med mittpunkter i origo.
Det gör att jag kan kallas x=2cost och y=2sint för den större och x=(1/2)*cost och y=(1/2)sint.
Sätter in h(2cost,2sint)= 2*2*cost*sint- ln1= 2*sin2t
h’t=4cos(2t)=0. Vilket ger mig t=pi/4 och 3pi/4, se uträkning nedan. Gör motsvarade för den lilla ringen. Vart någonstans är det jag gör fel?
Tack!
Till att börja med: Har du ritat upp området D? (Det är fullt möjligt att det finns nånstans inne i skuggorna, men mina gamla ögon ser det inte.) Funktionen f(x,y) ser ut att vara kontinuerlig, så största och minsta värde kan antingen vara ett lokalt mximum/minimum inne i omrädet, eller ligga på randen.