6
svar
147
visningar
Fler.dim, Variabelbyte i dubbelintegral (J.Månsson 7.23)
Hej! Har kört fast på följande uppgift:
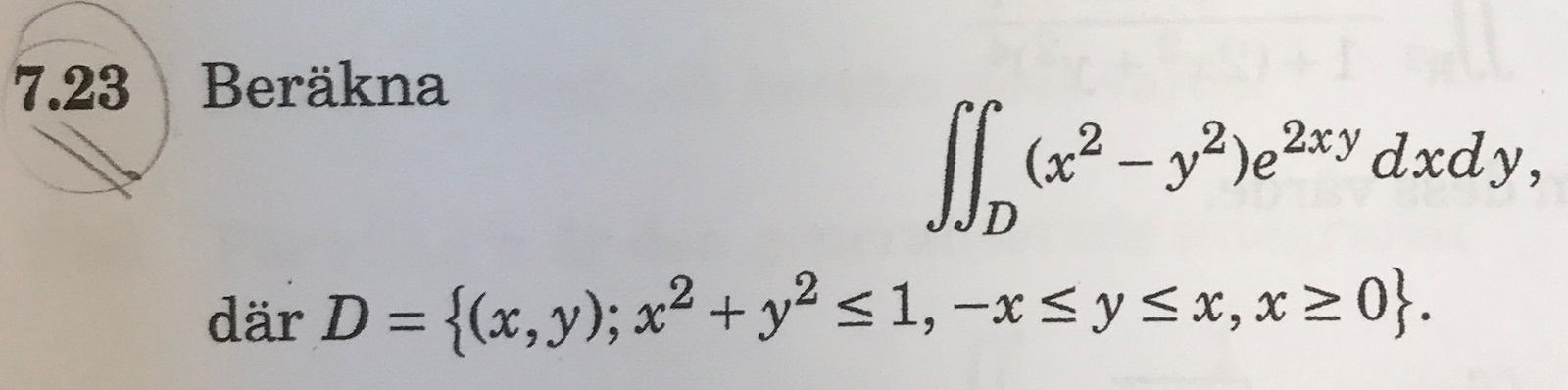
Där jag har gjort följande:

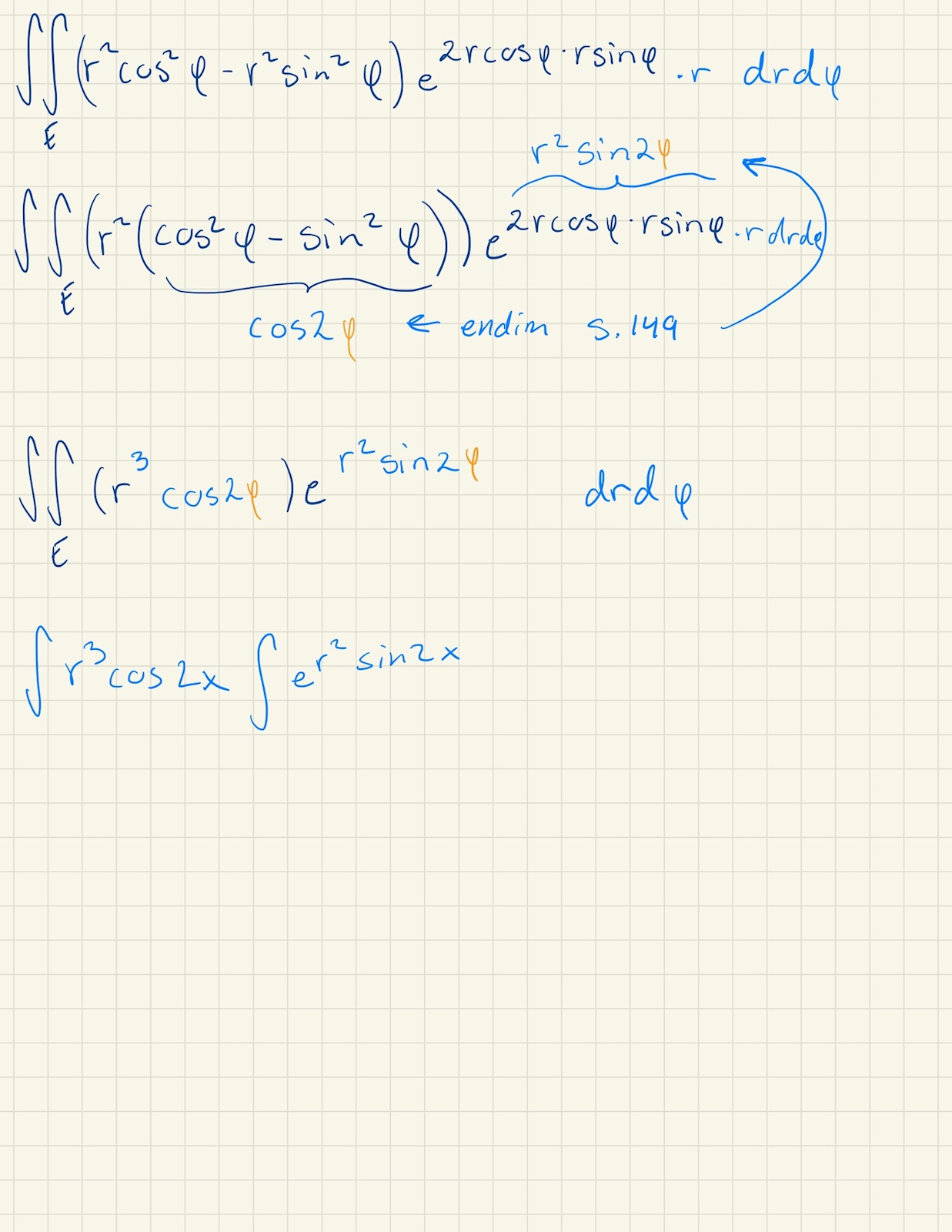
För att sedan köra fast...
Ser bra ut! Men du kan inte dela upp i 2 integraler när du inte kan faktorisera isär variablerna, så behåll den dubbla.
När jag tittar på din integreral och ser att sin finns instängd i en annan funktion (e), så tänker jag inre funktion, = ny variabel. Gör ett vanligt variabelbyte i en variabel där t=sinx så tror jag det löser sig.
ah, okej... testade både med men körde fast igen:
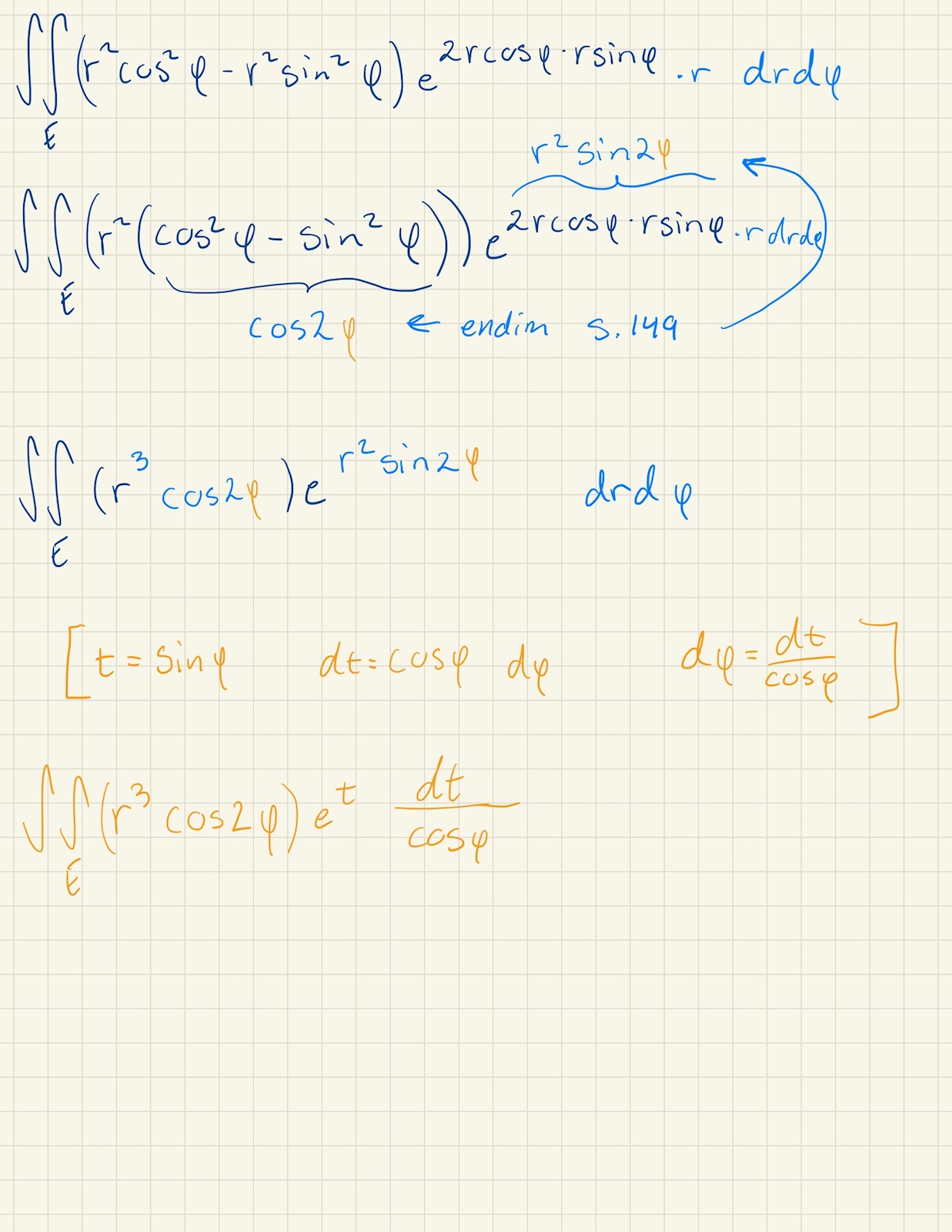
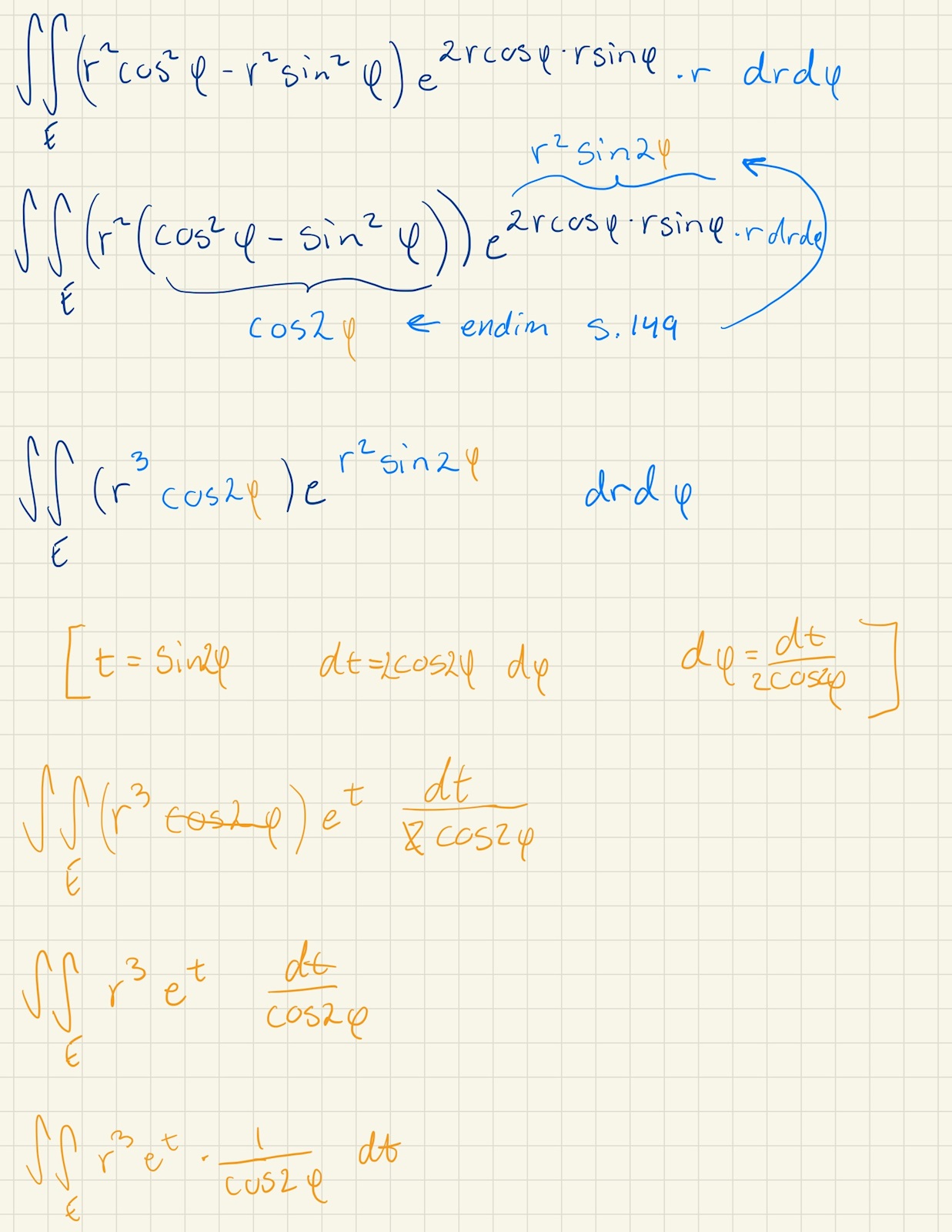
Varför har du bara strukit ena cos? 🤔 De tar ut varandra.
antar att vi snackar om bild nr. 2, så du menar att
Laguna skrev:.
Mmm, så jag har styrkt rätt?



