Fler.dim, Optimering - Visa att funktionen har ett min och max vädrde. (J.Månsson 5.32)
Hej! Har lite problem med följande uppgift:
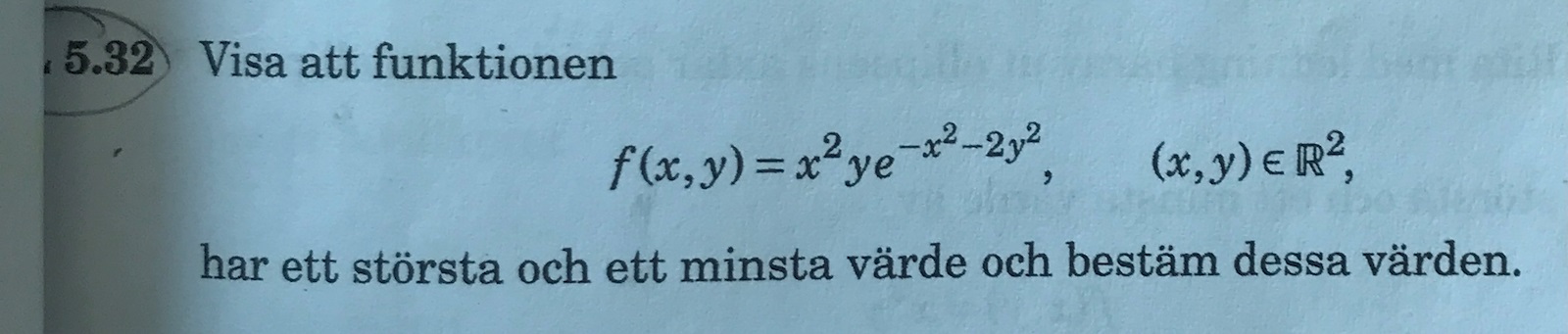
Där jag till viss del har kollat i lösningsförslaget förstår majoriteten men det är följande förenkling som jag inte förstår:
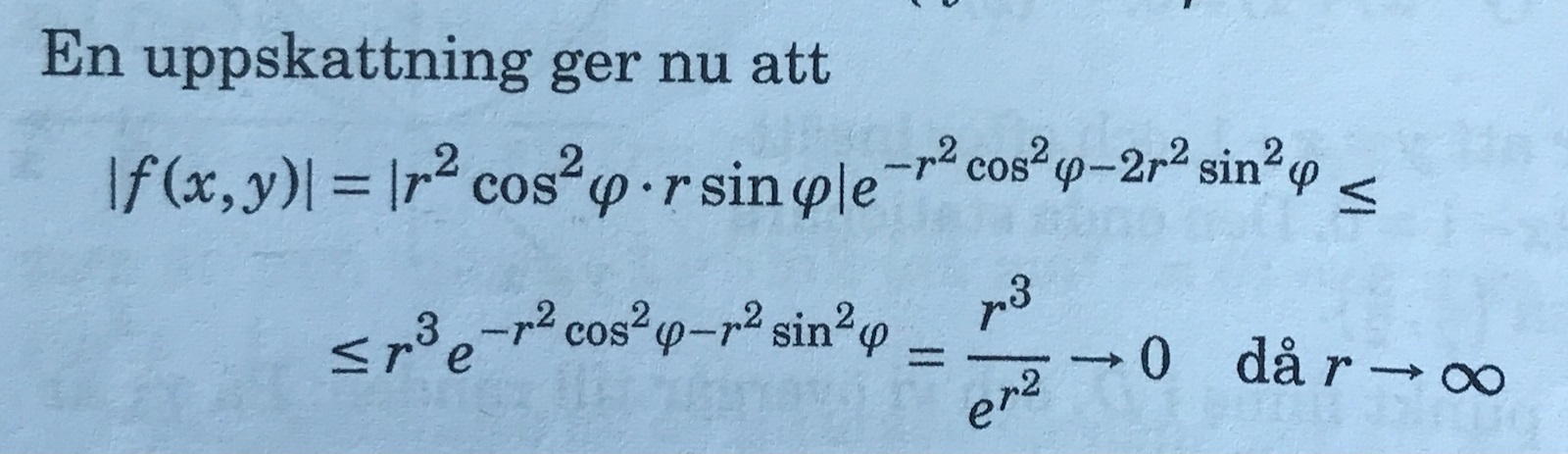
Där jag har gjort följande:

Vid första olikhetstecknet adderar de r^2sin^2(phi) till exponenten, vilket gör hela uttrycket större. Detta för att kunna använda den trigonometriska ettan cos^2(phi) + sin^2(phi) = 1.
Hej, okej men det måste väl adderas till flerställen? /någon form av kompensation för att vi har nu faktist ändrat värdena? Gjorde i alla fall följande:

Om du vill kan du lägga till ytterligare ett steg
Om det finns något -tecken här som du tycker inte stämmer, bara skriv.
Bedinsis skrev:Om du vill kan du lägga till ytterligare ett steg
Ahhh! Tack för förtydligandet! Men vad händer mellan dessa två?
Vad som händer är att man tittar på det som står innanför absolutbeloppet, konstaterar att det står
r3*[några trigonometriska termer]
och att [några trigonometriska termer] aldrig blir större än 1 eller mindre än -1, så tar man absolutbelopp på dem kommer det som mest bli 1, varmed man kan säga att det innanför absolutbeloppet understiger eller är lika med |r3|
Bedinsis skrev:Vad som händer är att man tittar på det som står innanför absolutbeloppet, konstaterar att det står
r3*[några trigonometriska termer]
och att [några trigonometriska termer] aldrig blir större än 1 eller mindre än -1, så tar man absolutbelopp på dem kommer det som mest bli 1, varmed man kan säga att det innanför absolutbeloppet understiger eller är lika med |r3|
Just det, såklart! Tack!
Men förstår däremot inte helt det med att man kunde addera "lite hur man ville"
Det är en olikhet, så du kan alltid göra den större sidan av olikheten större, utan att bryta olikheten.
Kolla nedan steg:
Bedinsis skrev:
Här multiplicerar vi den större sidan (HL) med något som är större eller lika med 1. Därmed kommer det nya HL vara större eller lika med det gamla HL, och olikheten gäller fortfarande.
Aha! Då hänger jag med, tack!



