Fler.dim, Generaliserade dubbelintegraler (J.Månsson 7.32)

Det blir lite fel när du bestämmer den primitiva funktionen arctan(xy). Kom ihåg att vi måste hantera konstanten x (eller den inre funktionen xy om du så vill) när vi bestämmer denna primitiva funktion.

Hummm, tänker ju att när jag deriverar arctan(xy) så ska det bli det som det blev innan den primitiva funktionen bestämdes. Men inte riktigt säker på att jag ser den inre funktionen/förstår hur jag hade applicerat samma tankesätt angående den inre funktionen. Då xy' är y (då den deriveras med avseende på x) borde då den primitiva funktionen av xy bli $\frac{y^2}{2}x$ ?

Du sa att den primitiva funktionen till $\frac{1}{1+x^2y^2}$ är $\arctan (xy)$.

Men vi kan nu derivera $\arctan (xy)$ och få $x\frac{1}{1+x^2y^2}$ alltså stämmer det inte. Ser du vad den primitiva funktionen behöver bli?

Hej! Nu tror jag att polletten kanske börjar trilla ner... gjorde följande: 

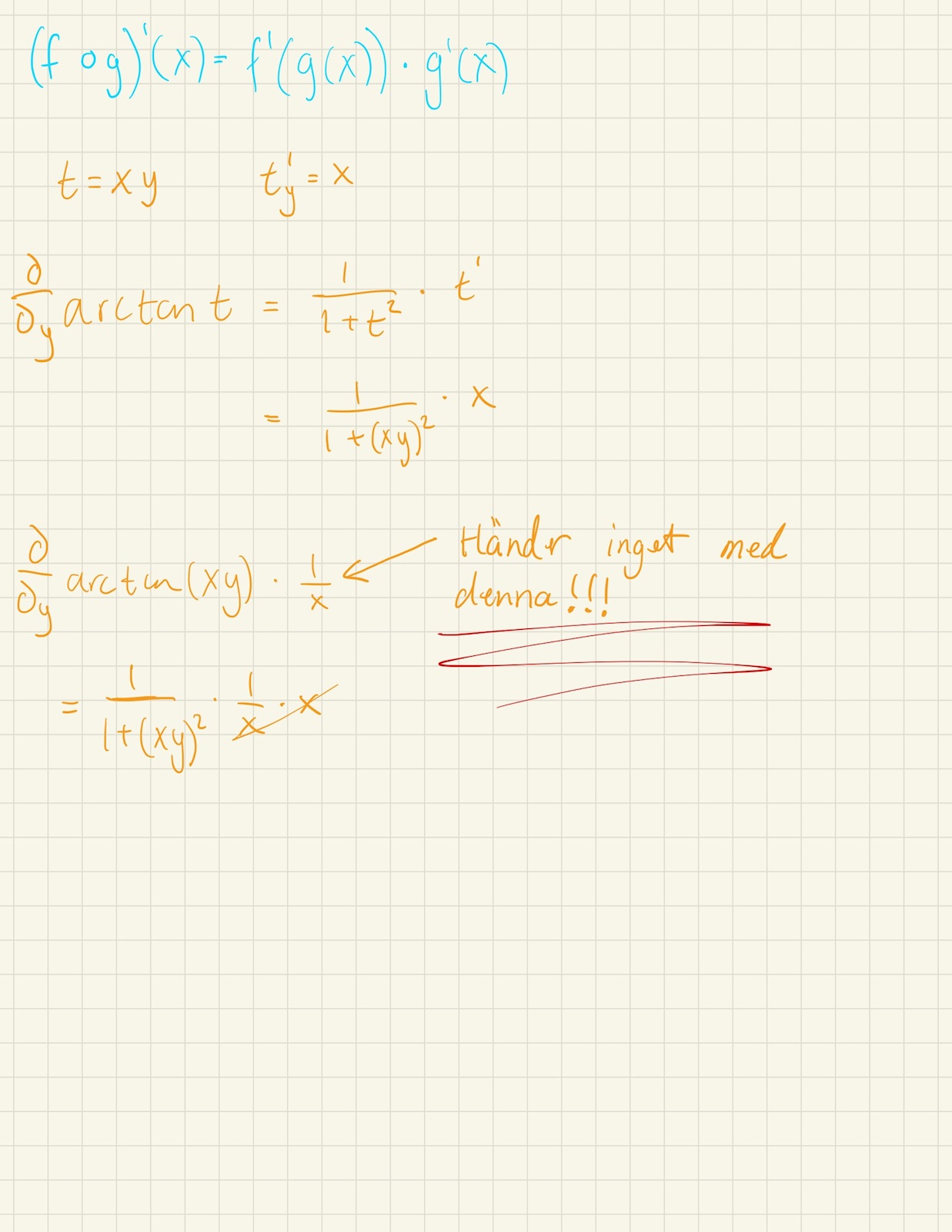
Däremot undrar jag om "strategin" är då att var gång derivera sitt resultat för att kunna "kompensera för den inre derivatan"? (till slut kanske man bara helt enkelt ser det)

Derivering och integrering är motsatta operationer, och kedjeregeln kan tillämpas på båda. På samma sätt som du multiplicerar med inre derivatan när du deriverar bör du dividerar med inre derivatan när du integrerar. Dock gäller det att den inre derivatan är en konstant, annars funkar det ej.

Personligen gillar jag att derivera den primitiva funktion jag tagit fram för att säkerställa att den är korrekt.

Toppen! Tack!