Fler.dim. Extenta - Differentsialekvation
Hej!
Jag har lite problem med följande fråga:
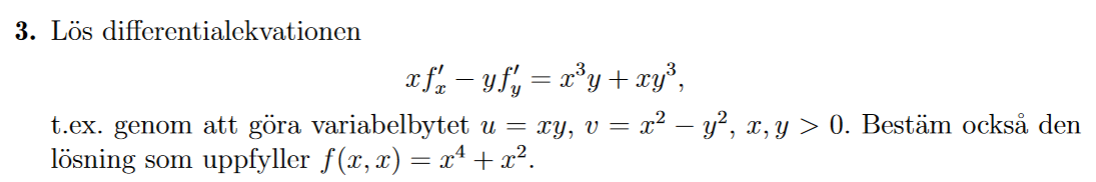
Där jag kommer hit:
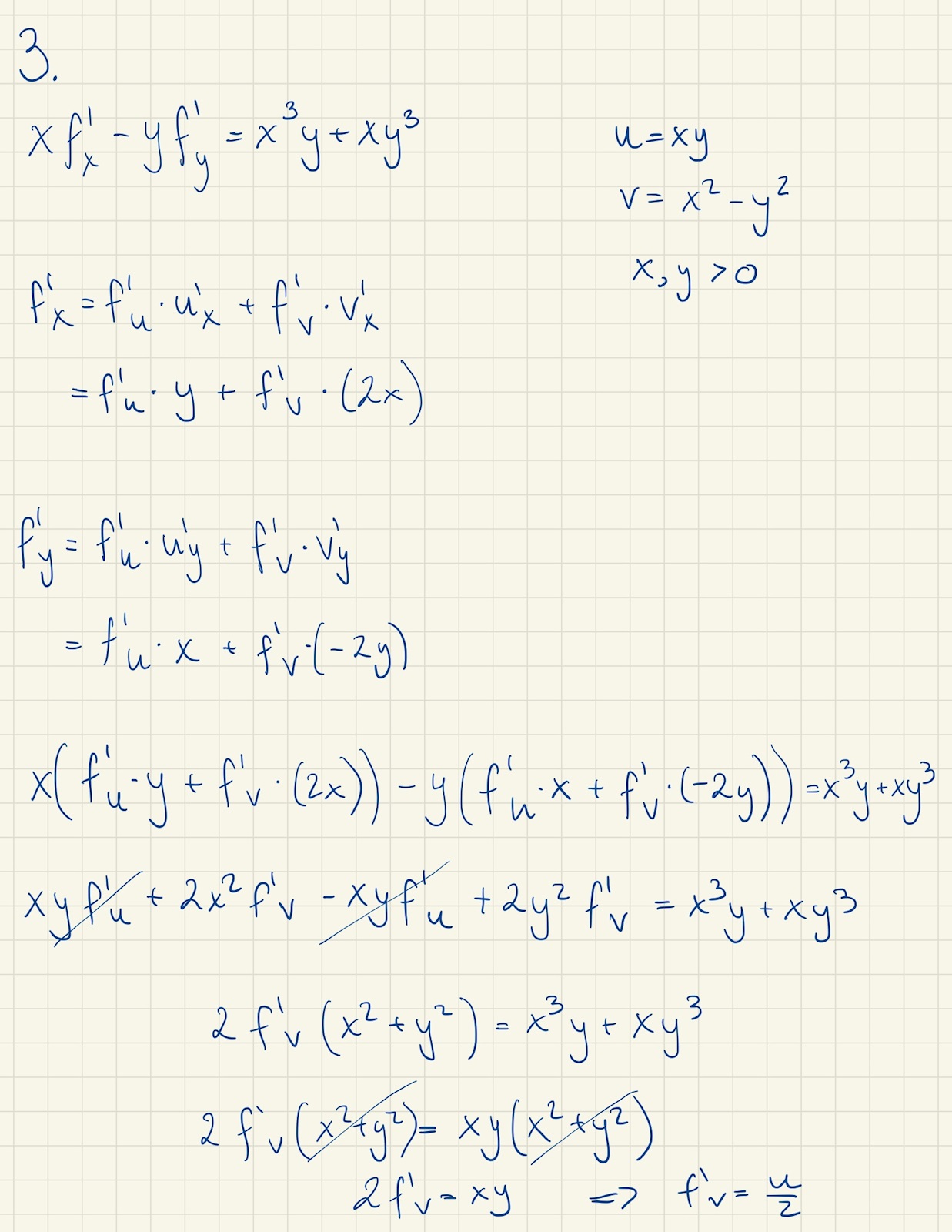
Sedan blir jag vilsen...
Lösningsförslaget efter detta förstår jag dessvärre inte heller:

Där jag speciellt inte förstår vart "v" kommer ifrån i f(x,y)=12uv+φ(u)
Du har kommit fram till att fv'. Nu ska vi integrera uttrycket med avseende på v samtidigt som vi betraktar u som en konstant.
Hade du studerat uttrycket hade det förmodligen känts mer bekant.
Om du integrerar uttrycket med avseende på v (u är en konstant) får du alltså
Där C är en integrationskonstant som kan bero av , av bekvämlighet skriver vi istället
Därmed gäller
Om du deriverar det uttrycket får du exakt
Hänger du med?
Jaaaa! Tack!
En annan fråga kom dock upp när jag försöker förstå resten av lösningen:
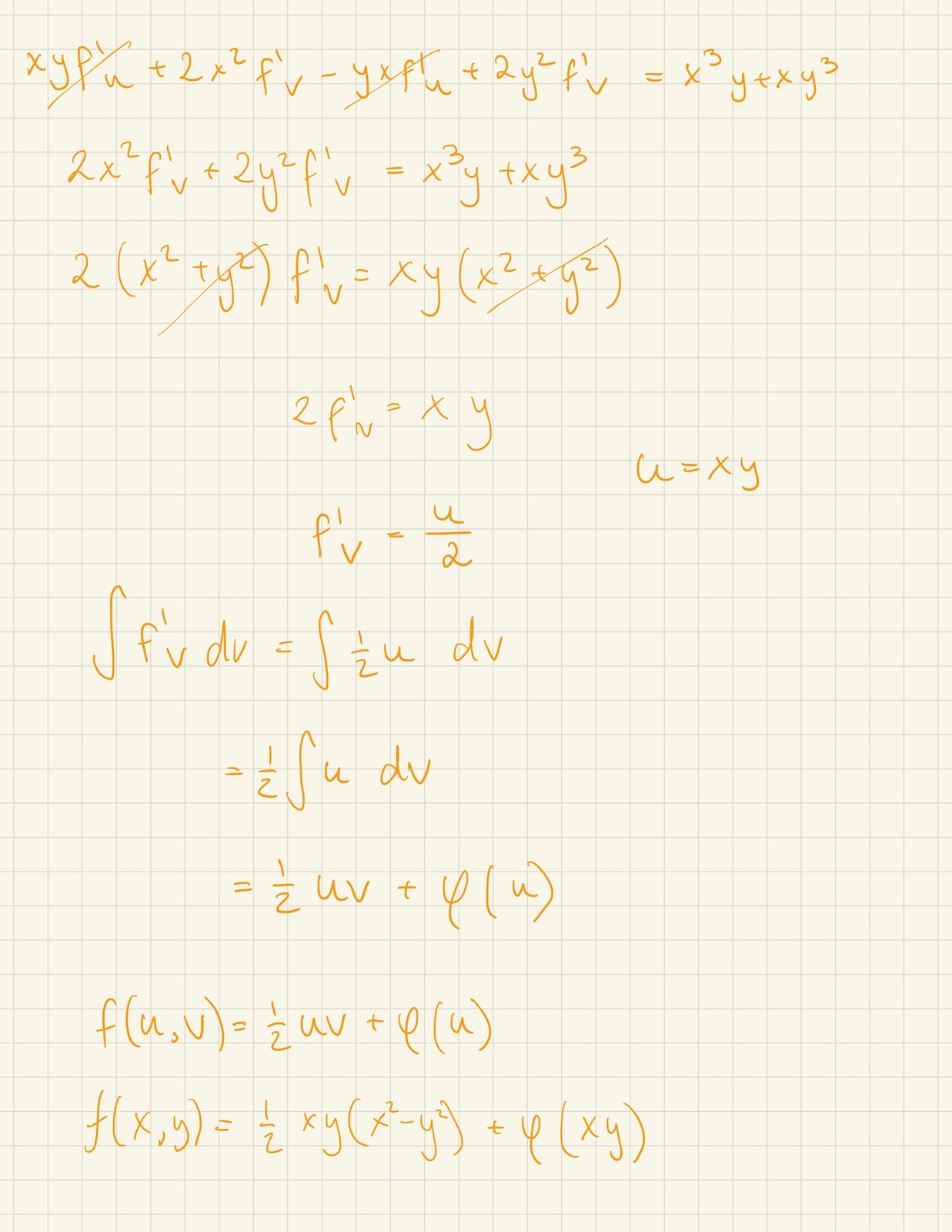
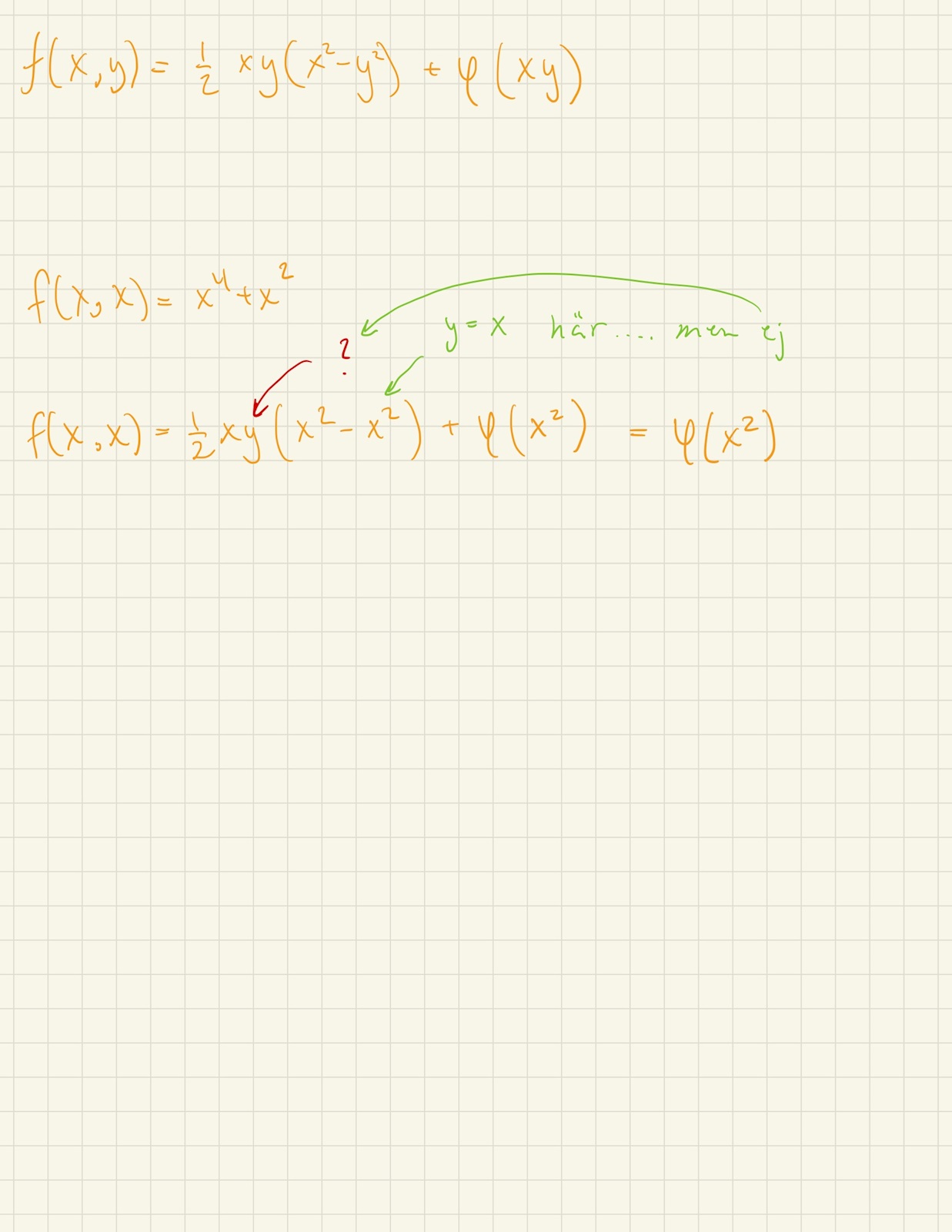
(se röda och gröna pilar)
Skrivfel.
Jaha, tack!


