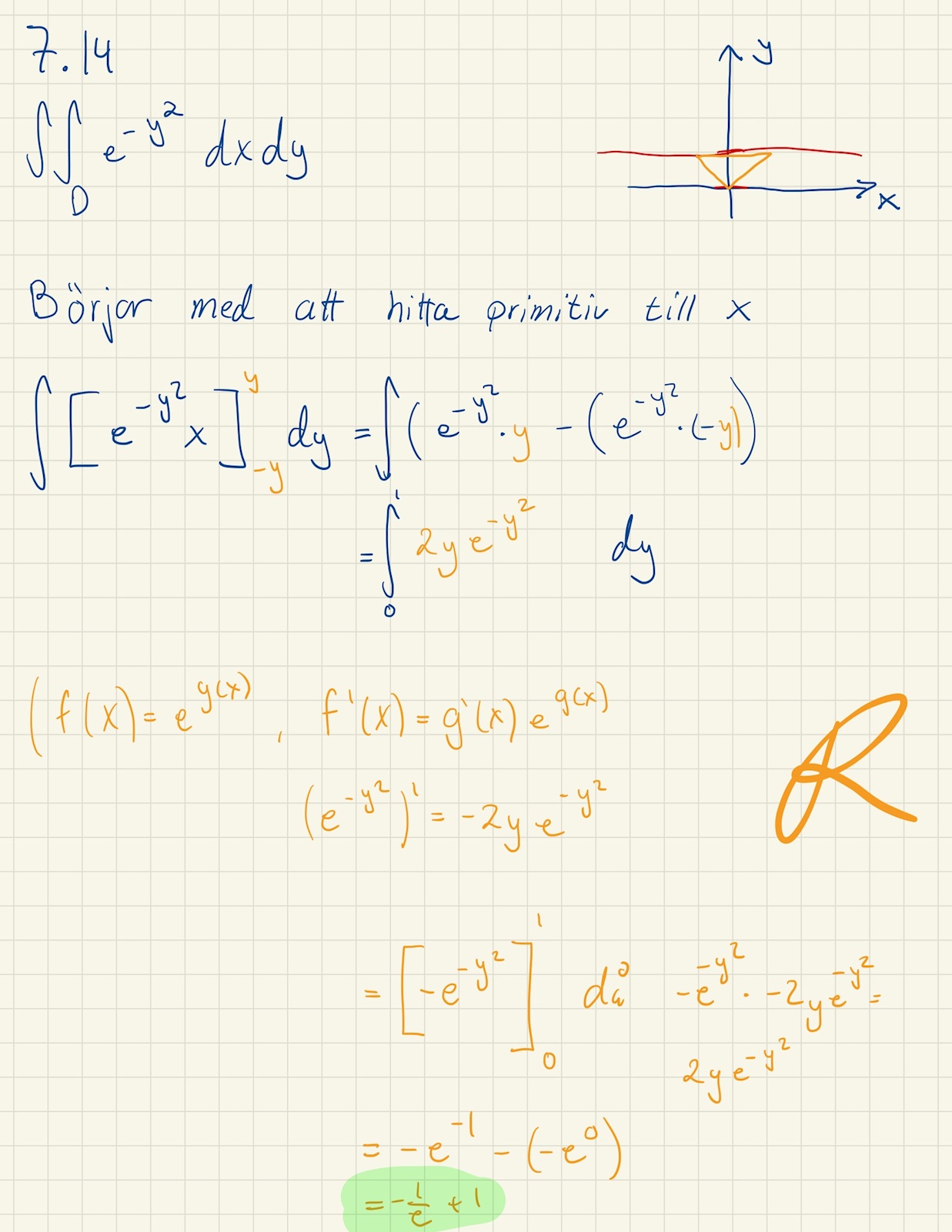Fler.dim, Dubbelintegraler (J.Månsson 7.14)
Hej! Har kört fast på följande uppgift:
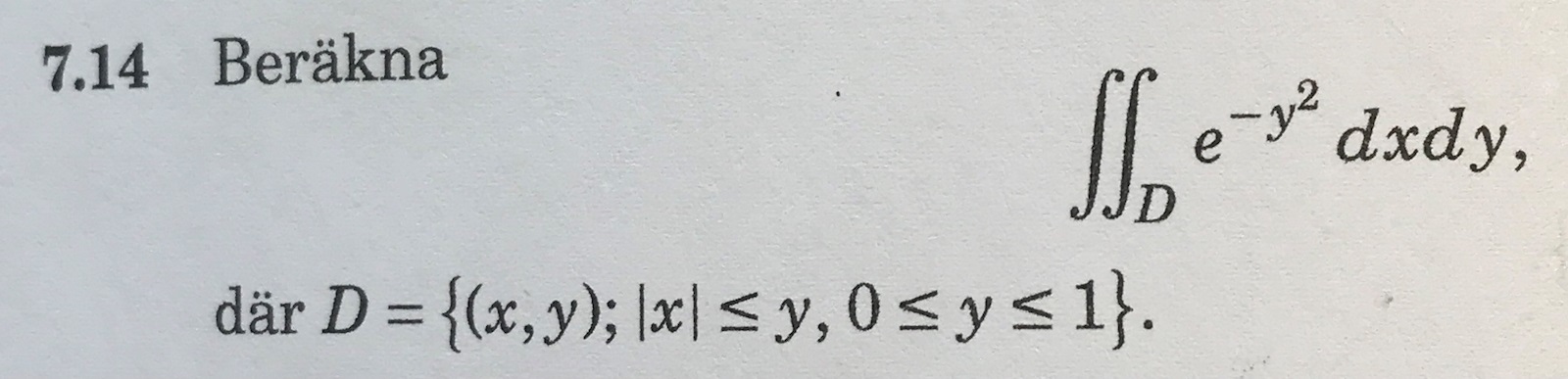
Där jag har gjort följande: 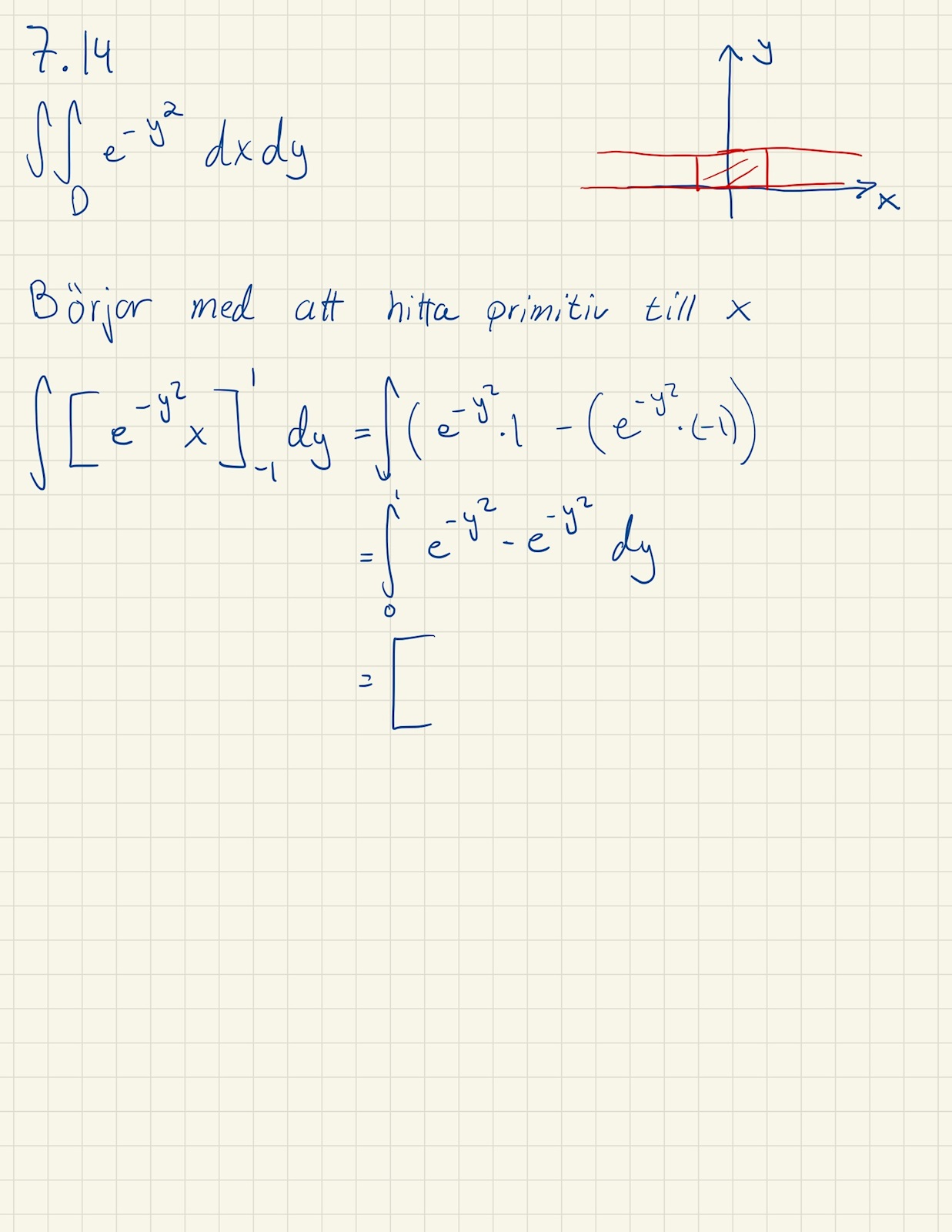
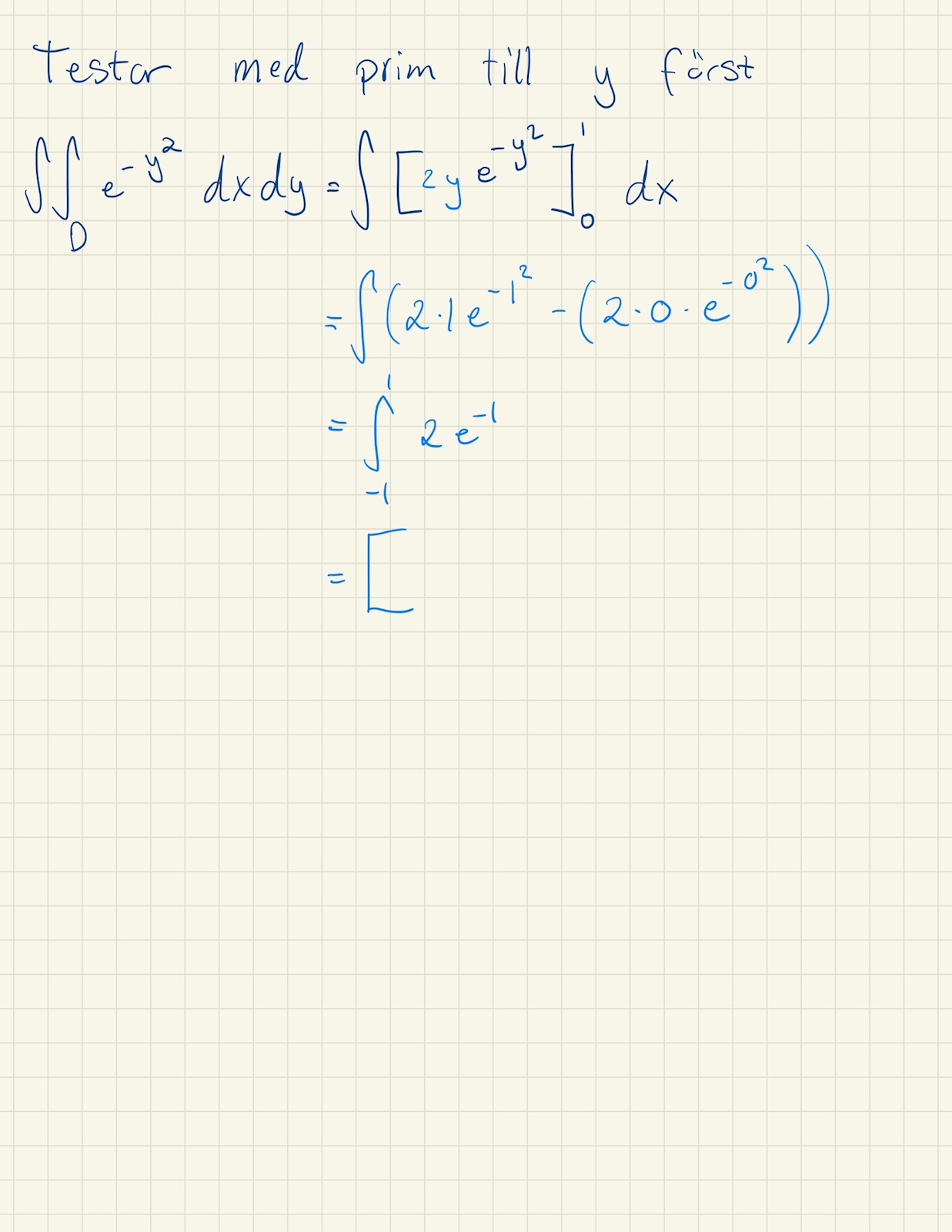
Där facit säger 1-e^-1 vilket tyvärr inte är det jag får... Någon som kan hjälpa mig att se vart jag har gjort fel?
Du vill nog se över integrationsgränserna. Området D blir inte rektangulärt. Punkten (1, 0) ligger väl t.ex. inte i D?
Jag tror sedan att du vill integrera med avseende på x först.
Gustor ska ha all cred för detta; integrationsområden som bildas av olikheter kan vara lite luriga ibland. Ett tips är att använda en programvara för att se vilket område som spänns upp. För domän i 2D kan Desmos vara ett bra hjälpmedel:
https://www.desmos.com/calculator/t2gpqndrc9
Jaha! Okej! Då är jag med på gränserna, däremot har jag lite problem med den primitiva funktionen, har gjort följande:
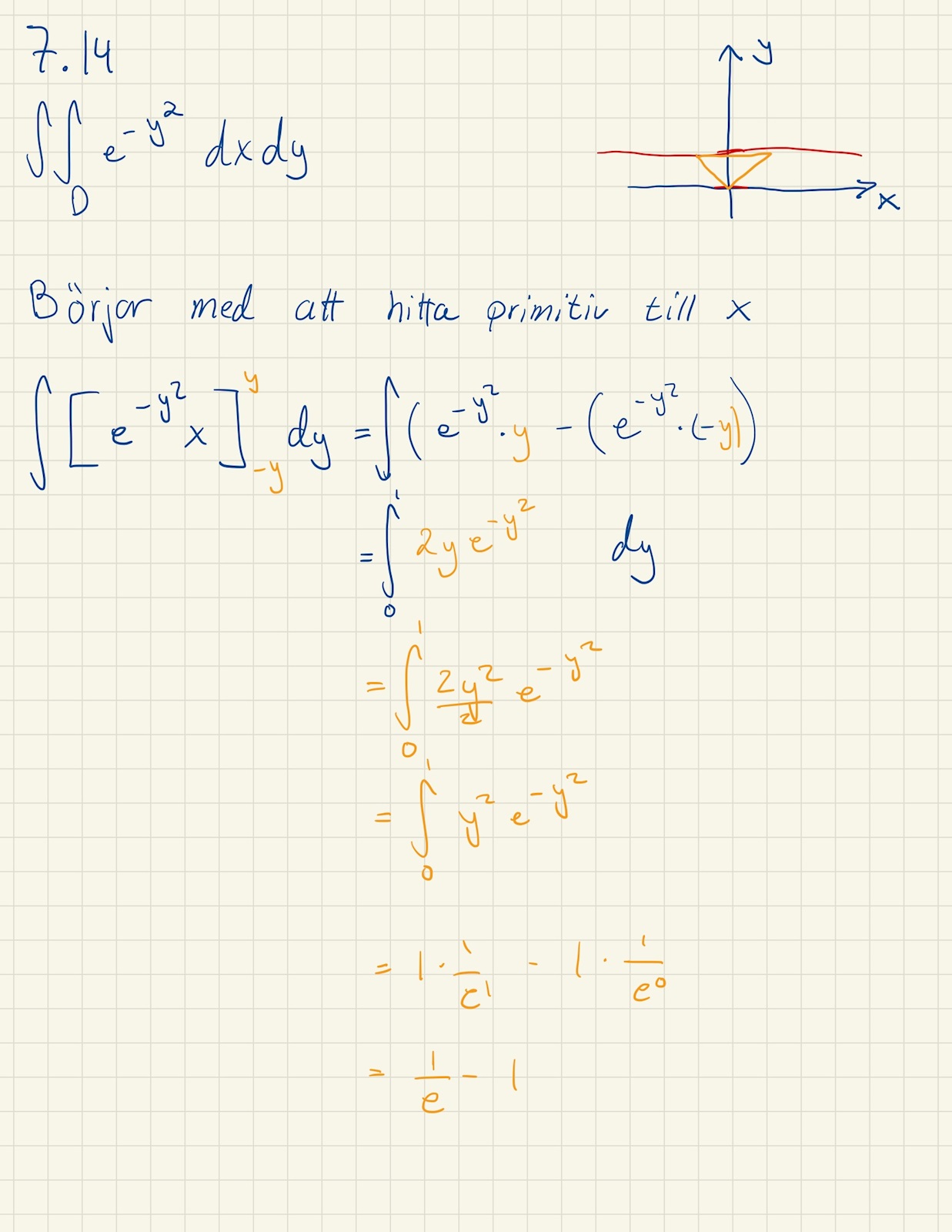
Jag hänger inte med på det sista riktigt, en primitiv funktion är väl -e^(y^2)? Så integralen blir -e^(-1) -(-1) = 1 - 1/e.
Humm, ser att jag hade glömt [] såhär blir det då:
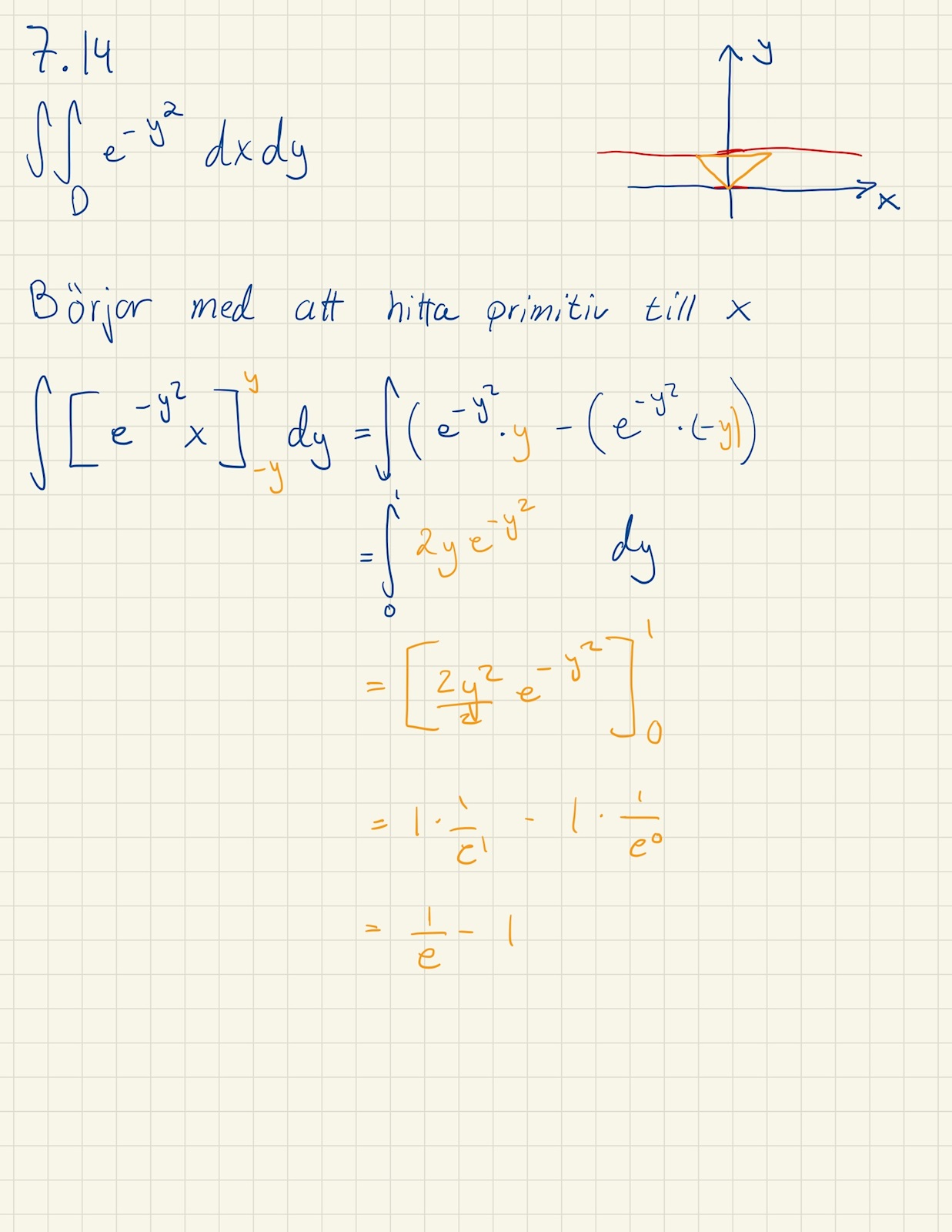
Din primitiva funktion är fortfarande fel.
Hummm, okej.... Skulle du kunna förklara lite mer ingående hittade i boken ett exempel för men när jag testade med variabelbytet fick jag inte till det...
Absolut. Om och , så är . Kedjeregeln ger att
Generellt så gäller att om för någon deriverbar funktion så är .
Exempelvis är .
Har man ett uttryck som , kan man därför notera att nästan är derivatan av , så när som på ett minustecken. Det leder en till att hitta den primitiva funktionen .
ahhh! Tack löste det nu! :)