Fler.dim, Beskriv funktionen med nivåytor. (J.Månsson 3.10)

Hej! Jag har lite problem med följande uppgift:

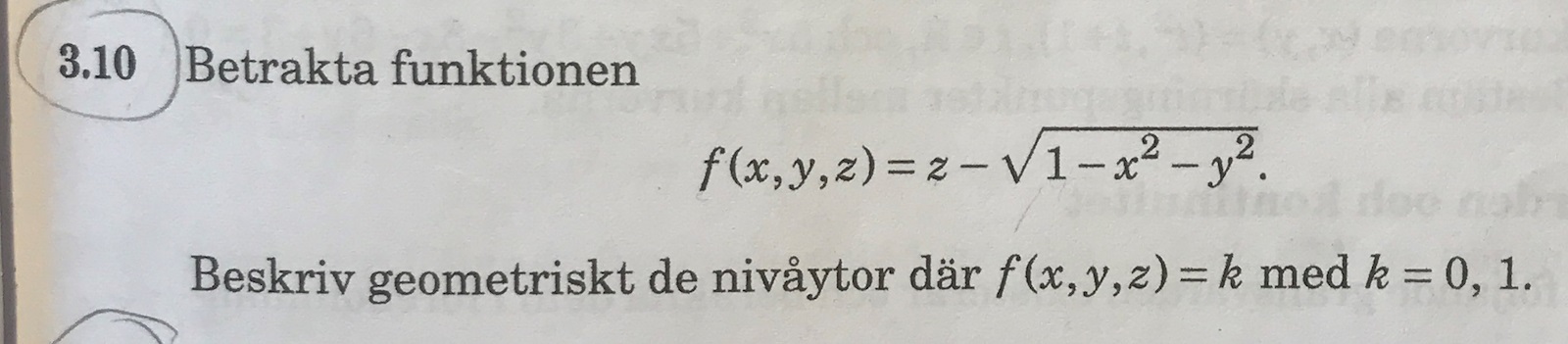
Där jag har gjort följande:

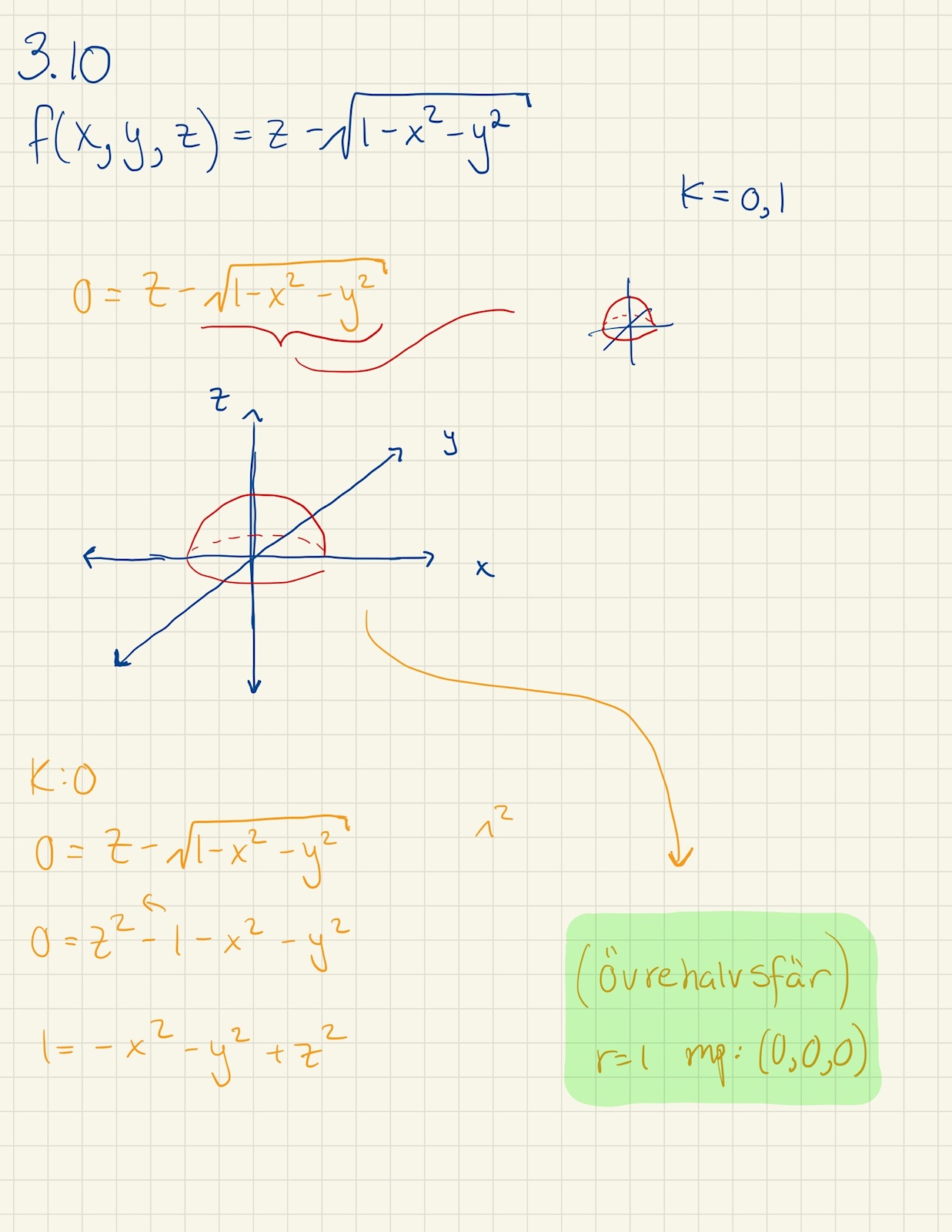
Där k=0 fallet har blivit rätt men när jag försöker med k=1 blir det fel... Vet inte riktigt hur jag ska lösa då k=1, någon som kan hjälpa mig på traven?

Om $f (x, y, z) = 0$ , så är $z = \sqrt{1 - x^{2} - y^{2}}$ , dvs. $z^{2} = 1 - x^{2} - y^{2}$ , eller $x^{2} + y^{2} + z^{2} = 1$ . Känner du igen den ekvationen?

Om $f (x, y, z) = 1$ fås istället att $x^{2} + y^{2} + {(z - 1)}^{2} = 1$ . (Om $1 = z - \sqrt{1 - x^{2} - y^{2}}$ så är $\sqrt{1 - x^{2} - y^{2}} = z - 1$ .) Hur skiljer sig detta geometriskt från den första?

Tänk på att $\sqrt{1-x^2-y^2}$ ställer direkta krav på $\left|x^2+y^2\right|$ samt därmed indirekt på z även i den andra deluppgiften.

Gustor skrev:
Om $f (x, y, z) = 0$ , så är $z = \sqrt{1 - x^{2} - y^{2}}$ , dvs. $z^{2} = 1 - x^{2} - y^{2}$ , eller $x^{2} + y^{2} + z^{2} = 1$ . Känner du igen den ekvationen?

Om $f (x, y, z) = 1$ fås istället att $x^{2} + y^{2} + {(z - 1)}^{2} = 1$ . (Om $1 = z - \sqrt{1 - x^{2} - y^{2}}$ så är $\sqrt{1 - x^{2} - y^{2}} = z - 1$ .) Hur skiljer sig detta geometriskt från den första?

Hej! Känner igen $x^{2} + y^{2} + z^{2} = 1$ (dvs. en sfär). Men hänger inte med på varför $z = \sqrt{1 - x^{2} - y^{2}} d å j a g v i l l h a d e t 0 = z - \sqrt{1 - x^{2} - y^{2}}$ (ser att det går att "slänga över" roten ur uttrycket, men det är där felet kommer i k=1).

Som svar på din andra fråga, att det blir en förskjutning i mittpunkten dvs. (0,0,1)?

Om du använder det jag skrev i parentesen efter f(x, y, z) =1, funkar det då? Du stuvar om så att rottecknet är ensamt på ena sidan och sedan kvadrerar.

Notera också som Daniel skrev att ekvationen förvisso beskriver en sfär (som är förskjuten som du säger då k=1) men du har samtidigt implicita begränsningar på z som uppstår från att det som står under rottecknet inte kan vara negativt. Ekvationen f(x, y, z) =0 är ekvivalent med x^2 + y^2 + z^2 = 1 för de värden x, y, z då f(x, y, z) är definierat.

Hej gjorde nu såhär:

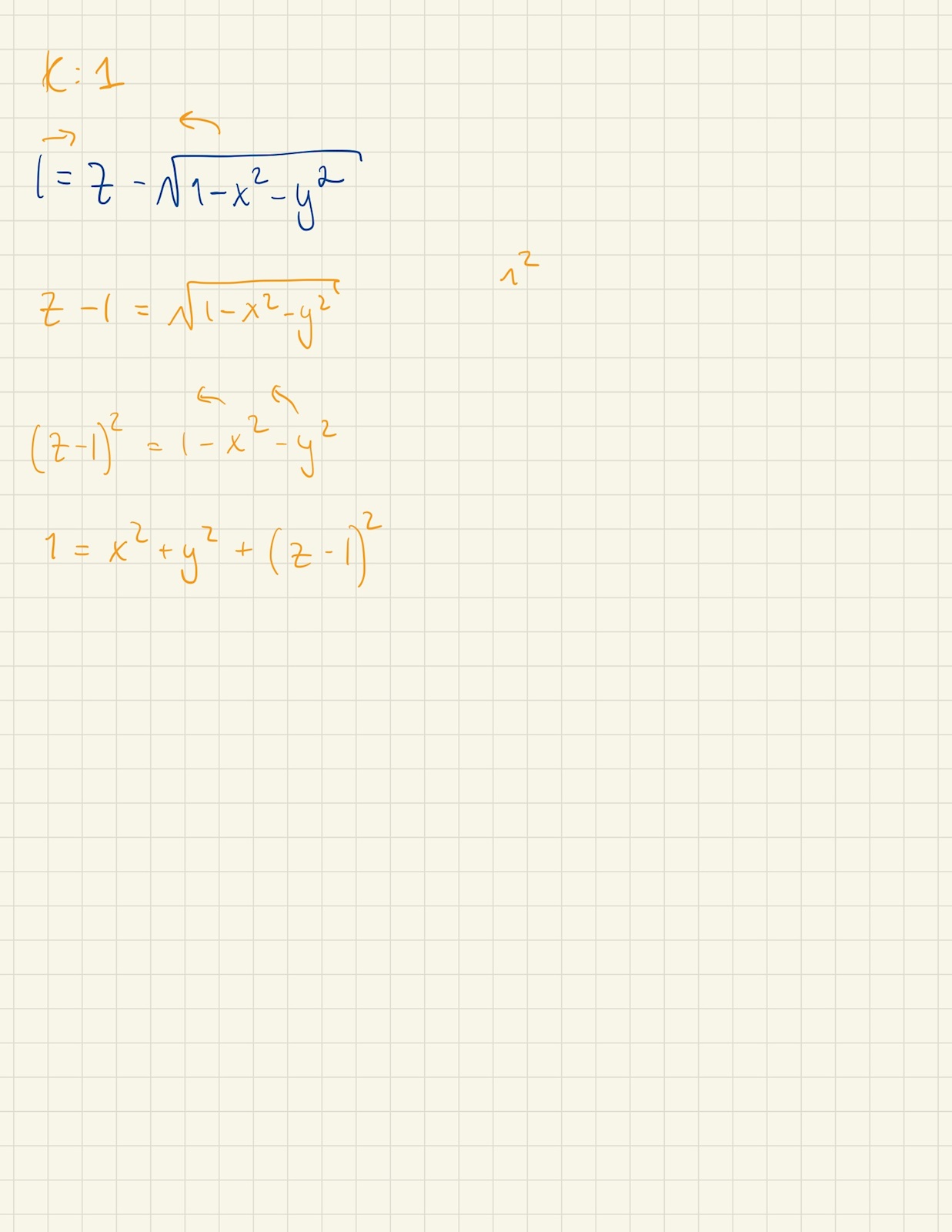
Så hur när man kvadrerar båda uttrycken spelar alltså roll?

Däremot hänger jag inte med på "implicita begränsningar på z som uppstår från [...]" (förstår att x,y inte får ge ett negativt uttryck).

Om det som står under rottecknet inte kan vara negativt, så kan inte x^2 + y^2 vara större än 1. Eftersom det är en summa av två kvadrater, kan det inte heller vara negativt. Så x^2 + y^2 ligger mellan 0 och 1. Så 1 - x^2 - y^2 ligger mellan 0 och 1. Alltså måste hela rotuttrycket ligga mellan 0 och 1. Det betyder att om f(x, y, z) = 0, så måste z också ligga mellan 0 och 1. Vi kan alltså konstatera att f(x, y, z) = 0 är ekvivalent med x^2 + y^2 + z^2 = 1 och z >= 0. Geometriskt bildar dessa två ekvationer en övre halvsfär.

När f(x, y, z) = 1 sker något liknande.

Okej, tack!

Svara

Visa senaste svar