Fler.dim, Avgör största och minsta värde. (J.Månsson 5.15)
Hej! Har lite funderingar på följande fråga:
Där jag har gjort följande:
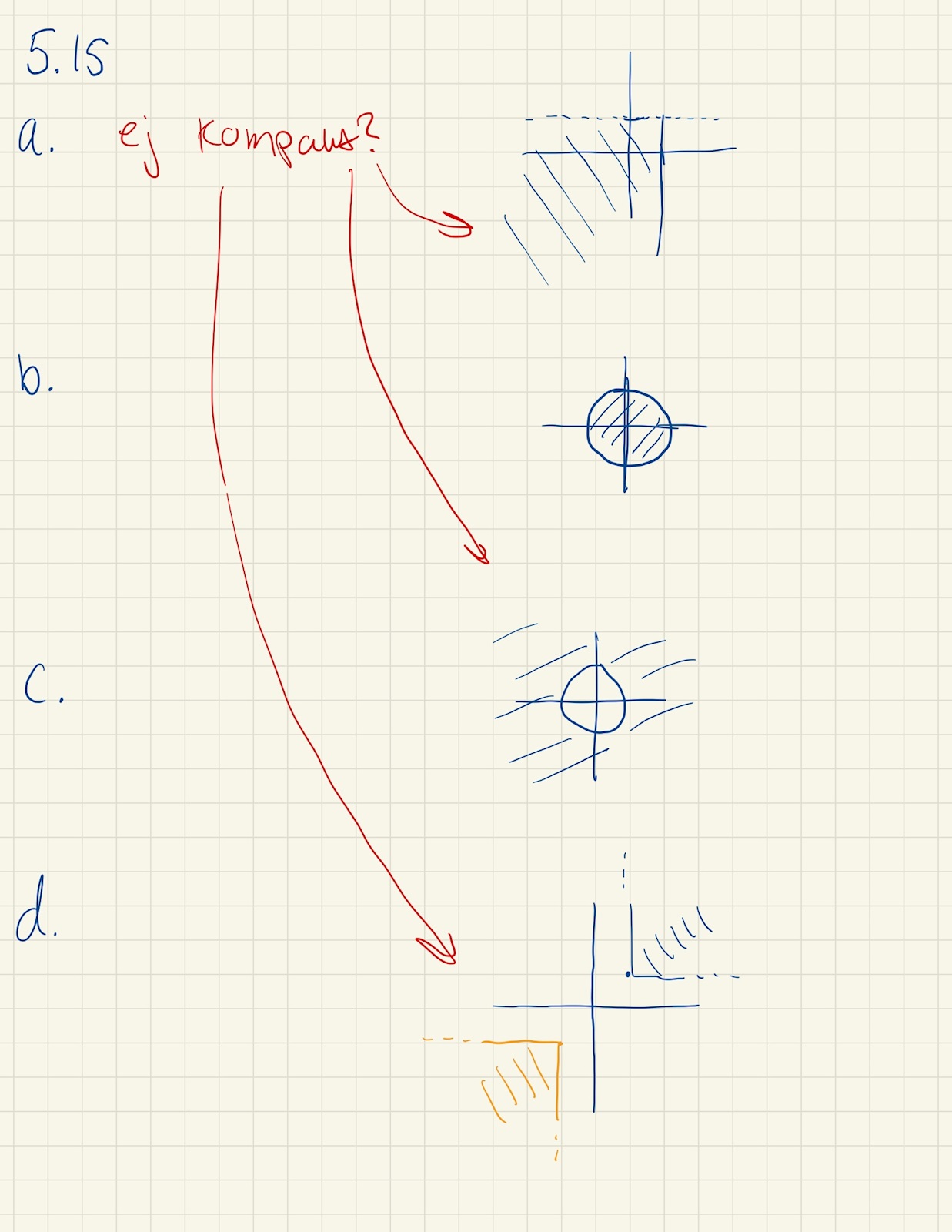Så som texten i rött säger, är a,c och d kompakta? (i min värld är dem inte det, och det kanske var det hela uppgiften gick ut på att avgöra, men känner mig osäker)
En känd sats säger att en mängd i Rn är kompakt om den är sluten och begränsad.
a är inte sluten, således ej kpt
b och e uppfyller båda kraven och är därför kompakta.
c och d är inte begränsade och alltså ej kompakta.
Mmmm, är kanske lite förrvirrad för jag förväntade mig "kompakta områden" då kapitlet handlar om dessa, tack!
Med "Områden" torde i detta sammanhang menas delmängder av R2 så satsen jag hänvisade till gäller i din situation.
En annan viktig sats som är verksam i den här uppgiften är: "Om en funktion är kontinuerlig på en kompakt mängd så antar den sitt max och sitt min på mängden." Notera att den bara gäller i EN riktning. Det är således INTE sant att om en kontinuerlig funktion antar sitt max och min på en mängd så är mängden kompakt. Ex: Låt f(x)=1 för alla x i R. Den antar sitt max och sitt min (=1) men R är inte begränsad och alltså inte kompakt.
