Fler.dim, Avgör karaktären. (J.Månsson 5.6)
Hej har lite problem att kvadrat komplimentera följande uppgift:
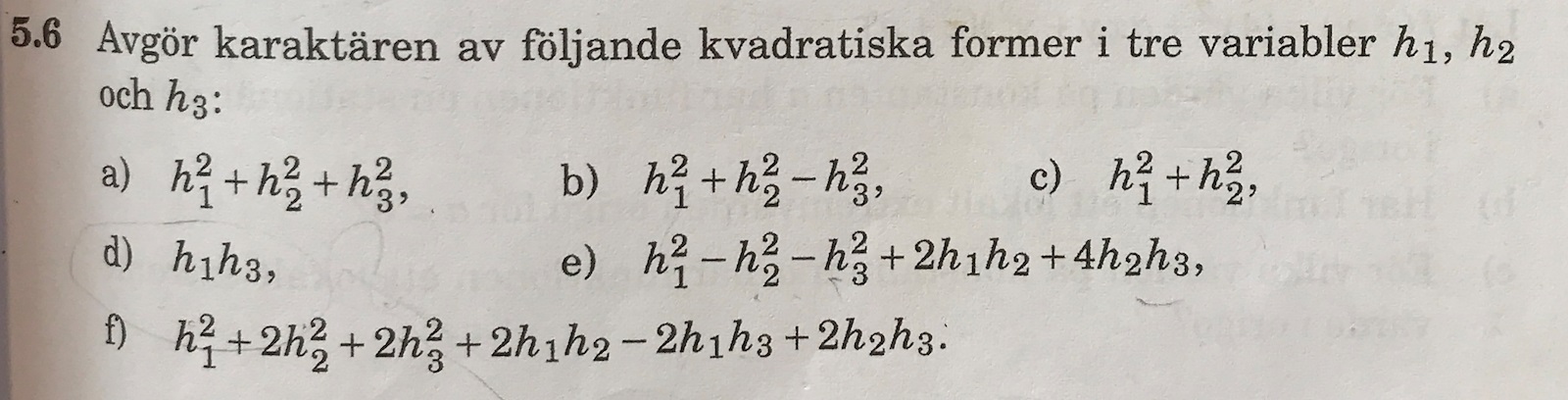
Där jag har gjort följande:

(ignorera det gula för närvarande, samt slutsatserna jag har dragit, insett att de är fel och att det är något fel med min KK som jag inte själv riktigt förstår...)
Den fåkunniges lösning (utan kvadratkomöettering):
a och c är summan av tre resp två kvadrater och kan alltså inte vara negativa ( om det reella tal åtminstone ).
b och e får olika tecken för (1,0,0) och (0,0,1) - alltså indefinita.
(återstår f)
Mmm, det stämmer så som du säger, men som jag tolkar kursboken med följande text:

Kan man endast göra det efter att uttrycket har kvadratkompletterats (?), var av jag kvadratkompletterar och får annat svar en facit.
Kvadratkomplettering gör man för att få formen omskriven så att den bara består av kvadrater, då kan man bestämma karaktären enkelt genom att jämföra koefficienternas tecken.
I a,b och c är det redan gjort, i d verkar det som en rejäl omväg men i e och f är det användbart.
Kanske har du använt en formel för kvadratkomplettering baklänges? Åtminstone i de första uppgifterna.
farfarMats skrev:Kanske har du använt en formel för kvadratkomplettering baklänges? Åtminstone i de första uppgifterna.
Möjligt, gör uttrycket till kvadrat, sedan kollar jag vad som blir "för mycket resp. för litet" och adderar/subtraherar så att det blir rätt uttryck. Problemet jag har är (förutsatt att mina kvadratkomplemetteringar är korrekta) är att de inte stämmer överens med bilden jag kommenterade tidigare. Om jag följer resonemanget i bilden ska uttrycken vara:
a. indefinit (olika tecken, eller gäller detta endast i själva kvadraten?)
b. indefinit -II-
c. indefinit
etc.
Anledningen till att göra kvadratkomplettering är att få den kvadratiska formen att skrivas som ett antal termer som är jämna kvadrater. Men i a,b och c är redan alla termer jämna kvadrater så att det finns ingen anledning att kvadratkomplettera, målet är ju redan nått
farfarMats skrev:Anledningen till att göra kvadratkomplettering är att få den kvadratiska formen att skrivas som ett antal termer som är jämna kvadrater. Men i a,b och c är redan alla termer jämna kvadrater så att det finns ingen anledning att kvadratkomplettera, målet är ju redan nått
Mmmm! Tack!

