Fjäderkraft som funktion av förlängningen och beräkna fjäderkonstanten?

Partykoalan skrev:

Vilket tillvägagångssätt är det rätta? 

Det är lite av en smaksak.

Det måste förstås vara så att kraften är noll vid jämviktsläget.

Å andra sidan finns det en viss osäkerhet i att bestämma exakt vid vilket x-värde jämviktsläget ligger.

Boken antar att linjen går genom origo även fast man ser att den inte gör det. Även den andra punkten som boken använder ser man är en ganska grov uppskattning.

Jag tycker du gör en mycket bättre lösning än boken om du gör en linjär anpassning med miniräknaren, och istället avrundar lite på slutet.

Jag tycker bokens lösningsförslag är jättedåligt. Istället för att försöka ta fram ett närmevärde genom att utnyttja alla uppmätta mätpunkter, som du gör, så använder boken två mätpunkter som varken är uppmätta i experimentet eller uppskattade med hjälp av linjen. 

JohanF skrev:

Jag tycker bokens lösningsförslag är jättedåligt. Istället för att försöka ta fram ett närmevärde genom att utnyttja alla uppmätta mätpunkter, som du gör, så använder boken två mätpunkter som varken är uppmätta i experimentet eller uppskattade med hjälp av linjen. 

Boken skriver "Vi bedömer att linjen går genom punkterna (90, 5) och origo."

Det är en rimlig bedömning men den handlar inte om den tryckta figuren.

Såhär tänker jag:

Facits lösningsförslag skulle såklart ha varit rimligt och godtagbart om det hade varit en elevlösning. Det som var speciellt bra i den elevlösningen var att det tydligt framkom vilket resonemang som förts, och vilka beslut som tagits vid beräkningarna. Men nu var detta ingen elevlösning (antar jag), utan en läromedelslösning. I en sådan lösning skulle det ha varit bra att visa kvalitet. Och det är detta som tråden handlar om. Det finns inget exakt svar eftersom uppgiften bygger på experimentella mätningar som man ser att de inte kan följa den fysikaliska modellen exakt. Men vilket lösningsförslag är bäst kvalitet?  

Då tycker jag att Partykoalans två lösningsförslag är bäst, och sist kommer facits lösningsförslag. Anledningen till att jag tycker det är att eftersom vi inte vet om det finns mätpunkter i Erikas mätserie där hon känner på sig att hon misslyckades totalt (isåfall kanske då det bästa hade varit att utesluta just dessa mätpunkterna ur mätserien), så måste det bästa vara om alla mätpunkter hanteras som om de hade haft ungefär samma osäkerhet. Dvs att räkna fram något slags medelvärde på k, precis som Partykoalan har gjort.

Det mest olyckliga med boken är att figuren och texten inte matchar med varandra. Sådant kan hända i produktionsprocessen men det skapar onödiga problem för elever och för lärare.

Det andra olyckliga är att kraften ges i newton med en massa siffror (som eleven ska bearbeta) medans det bara är tyngder på 100 gram, 200 gram, osv. 

Nuförtiden är det lätt att räkna ut en uppskattad linje med dator och därför är det bra att göra det. Tyvärr ger programmen sällan det uppskattade felet. Jag gjorde det med Logger Pro, får samma siffror som Partykoalan men får då också det uppskattade felet. Offset är 0,18 ± 0,10 newton, fjäderkonstanten 52,6 ± 1,6 N/m eller 53 ± 2 N/m.

Jag uppfattade frågan i första hand som vilken modell man skulle använda: ett allmänt linjärt samband eller en ren proportionalitet. Det är lite av en smaksak. Om man vill kan man försöka avgöra med ett $\chi^2$-test vad som är statistiskt sett mest lämpligt (fast jag har glömt hur man gör).

Om jag väljer en ren proportionalitet i Logger Pro blir fjäderkonstanten 55,3 ± 0,9 N/m.

I sådana här fal blir resultaten egentligen inte bättre med datorn än att rita för hand på millimeterpapper och att uppskatta linjen på ögat med en genomskinlig linjal.

Tack för era svar! Om man utgår från Hookes lag F=kl (delta l) så är grafen en rät linje som går genom origo. Jag antar att det är därför som boken antagit att linjen går igenom origo trots att den inte gör det. Kan det vara så ekvationen som miniräknaren tagit fram inte är i enlighet med Hookes lag då m-värdet, dvs. kraften måste vara noll?

Vi ser ju på miniräknarens funktion att m-värdet (dvs kraften) är 0 ,18 N? Hur ska man tolka denna "begynnelsekraft"? Vad föreställer den?  Kan man helt bortse från den eller ska man inkludera den kraften vid olika  beräkningar? 

Partykoalan skrev:

Vi ser ju på miniräknarens funktion att m-värdet (dvs kraften) är 0 ,18 N? Hur ska man tolka denna "begynnelsekraft"? Vad föreställer den?  Kan man helt bortse från den eller ska man inkludera den kraften vid olika  beräkningar? 

Den är 0,18 ± 0,10 N. Den procentuella statistiska osäkerheten är alltså mycket stor och det är inte osannolikt att det helt beror på slumpen att den termen finns.

Det kan vara bättre att göra den matematiska modelleringen utan denna term.

Men det beror lite på vad det var för fjäder. Vissa fjädrar går inte att trycka ihop eftersom lindningarna nuddar varandra i jämviktsläget. En sådan fjäder börjar bara bli längre vid en viss minimal kraft. I sådana fall måste denna konstanta term vara med.

Pieter Kuiper skrev:

Partykoalan skrev:

Vi ser ju på miniräknarens funktion att m-värdet (dvs kraften) är 0 ,18 N? Hur ska man tolka denna "begynnelsekraft"? Vad föreställer den?  Kan man helt bortse från den eller ska man inkludera den kraften vid olika  beräkningar? 

Den är 0,18 ± 0,10 N. Den procentuella statistiska osäkerheten är alltså mycket stor och det är inte osannolikt att det helt beror på slumpen att den termen finns.

Det kan vara bättre att göra den matematiska modelleringen utan denna term.

Men det beror lite på vad det var för fjäder. Vissa fjädrar går inte att trycka ihop eftersom lindningarna nuddar varandra i jämviktsläget. En sådan fjäder börjar bara bli längre vid en viss minimal kraft. I sådana fall måste denna konstanta term vara med.

 En annan trolig förklaring kan vara att Erica lagt nollnivån på sin linjal fel, så att linjalen visar fel hela vägen?

Hur som helst, varför använda en mätpunkt som inte ens är uppmätt, om det finns fem andra mätpunkter att utnyttja? 

JohanF skrev:

Hur som helst, varför använda en mätpunkt som inte ens är uppmätt, om det finns fem andra mätpunkter att utnyttja? 

Som jag förstår det handlar det om en annan figur än vad som blev tryckt i boken, en figur med en anpassad linje genom origo.

En sådan anpassning kan ha gjorts på ögat, gick genom origo och genom (90, 5). Den proceduren tar då hänsyn till alla fem mätvärden och är mer pålitlig än att bara använda ett enstaka mätvärde.

Så det är alltså tillåtet att använda funktionen som miniräknaren tagit fram i framtida liknande  beräkningar för att få fram ett noggrannare mätvärde? Alltså även om den allmäna funktionen F=kl utesluter m-värdet och utgår från att linjen går genom origo? Hur ska man gå till väga om man får en liknande funktion på ett prov? 

Partykoalan skrev:

Så det är alltså tillåtet att använda funktionen som miniräknaren tagit fram i framtida liknande  beräkningar för att få fram ett noggrannare mätvärde?  

Det borde vara tillåtet men det är inte alls säkert att det blir mera noggrant.

På prov ska man följa instruktionerna. Och instruktionerna ska inte vara förvirrade som den här sidan i boken.

I nedanstående figur kan man se vad som blir skillnaden med att använda Partykoalans ”miniräknarmetod” jämfört med facits tillvägagångssätt (Jag plottade i Excel). De blå prickarna är Ericas mätvärden, den blå streckade linjen är linjäranpassningan till Ericas mätvärden. Ekvationen för den blå linjen blir samma som Partykoalans miniräknare, dvs k=0.0526. Den blå streckade linjen ser dessutom _väldigt_ likadan ut som facits graf.

De oranga prickarna är de punkterna som facit _bedömde_ skulle vara bäst att använda, (0,0) och (5,90), och den oranga streckade linjen mellan dessa punkter får k=0.0556, dvs facits svar.

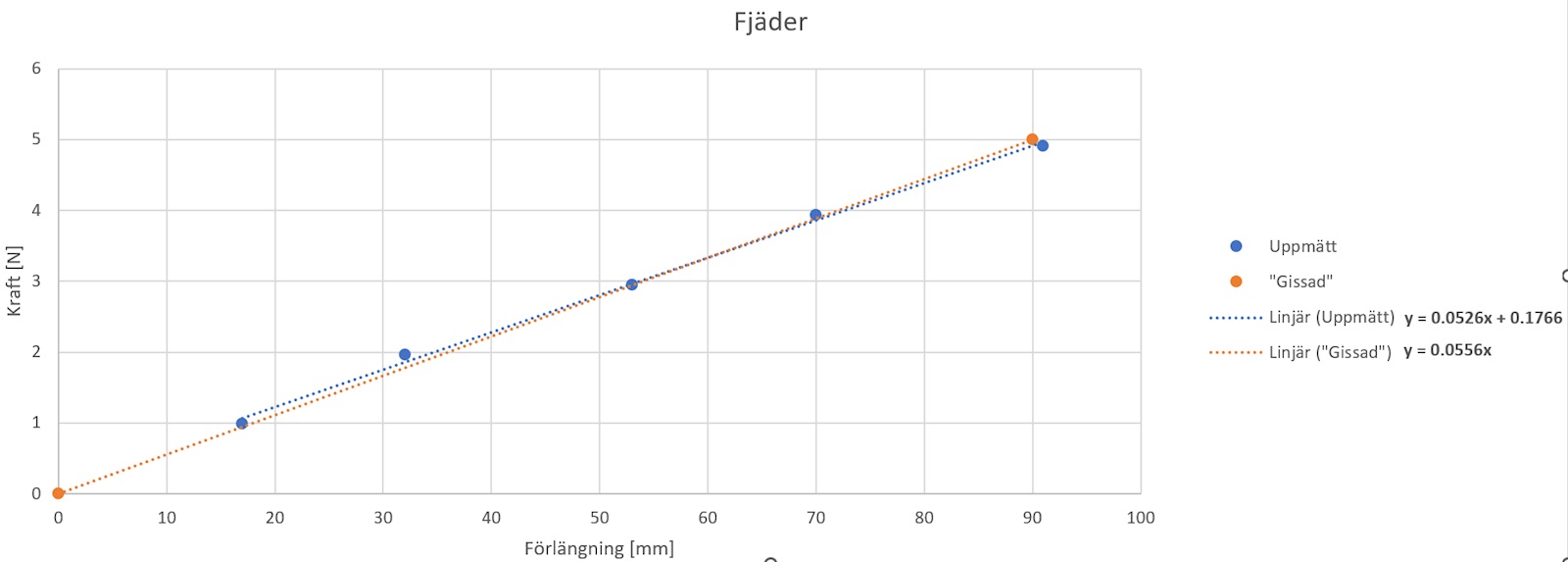
Tittar man lite närmare på dessa två linjer så kan man konstatera att Partykoalan använde ett tillvägagångssätt där man tror att varje mätning som Erica har gjort har ett litet mätfel, men man anser att alla hennes mätningar är värda att användas. Dvs man antar att närmast sanningen är att hon har gjort ungefär lika stort mätfel vid samtliga mätningar, och att linjen som stämmer ganska bra med alla mätpunkterna är mest sann.

Facit däremot, valde ett tillvägagångssätt som gjorde att Erikas andra mätning och hennes femte mätning fick tas mindre hänsyn till än hennes övriga mätningar. Om det är rätt eller fel är ingen som vet, och båda lösningarna tycker jag är godtagbara, med jag tycker Partykoalan övertrumfar facit.

Sedan, huruvida man löser uppgiften med linjärregression på miniräknaren eller drar linjen med ögonmått och linjal, spelar mindre roll. Den större skillnaden i tillvägagångssätt är ju att i ena fallet används Ericas mätvärden, i andra fallet gör man antagandet att Ericas mätserie måste kunna extrapoleras genom origo, på bekostnad av vissa av Ericas utförda mätvärden.

Men du Partykoalan, var inte orolig för att din linje inte går genom origo! Det är sällan den uppmätta verkligheten är lika exakt som den matematiska modellen. Det bästa hade ju förstås varit om b-frågan hade varit formulerad ”vilken fjäderkonstant har fjädern inom det längd-intervall som Erica mätte?”. Då hade i sluppit bry oss om vad som händer i origo. Alternativt om Erica även hade hunnit med att mäta en mätpunkt med fjäderförlängning noll. Men då hade vi förstås missat den här roliga utredningen!

Detta är vad jag får med två olika modeller i Logger Pro (den använder säkert minstakvadratmetoden):
Tyvärr kan jag inte färglägga linjerna, men linjen F = Ax går nästan precis genom punkten (90, 5).

Tack för er hjälp!