Fin icke-reel rot till ekvationen.
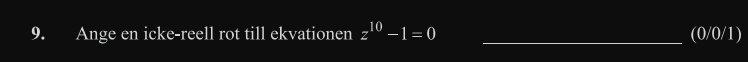
Om jag ställer upp två polära utryck lika med varandra, vilka krav måste stämma?
Har hört att de reela delarna måste vara lika med varandra, men de imaginära inte.
Ett komplext tal motsvarar en bestämd punkt i det komplexa talplanet.
För att två komplexa tal ska vara lika med varandra så måste båda talen motsvara samma punkt i det komplexa talplanet.
För att de ska motsvara samma punkt så måste både real- och imaginärdelarna vara lika.
Om de komplexa talen är skrivna på rektangulär form så finns det bara ett sätt att representera en specifik punkt i det komplexa talplanet.
Men ett komplext tal skrivet på polär form anges med hjälp av ett avstånd från origo (kallas även absolutbelopp) och en riktning (kallas även argument eller vinkel och avser motursvinkel mot den positiva delen av realdelsaxeln).
Absolutbeloppet (dvs avståndet) går inte att skriva på olika sätt, men riktningen (som anges med hjälp av argumentet) går att skriva på oändligt många sätt eftersom de trigonometriska funktionerna som används har en periodicitet på radianer (360°).
Det betyder att: och är lika med varandra, dvs motsvarar samma komplexa tal, om:
- , där är ett heltal.
Dvs
- absolutbeloppen måste vara lika stora
- argumenten måste antingen vara lika eller skilja sig åt med ett helt antal "varv".
Var det svar på din fråga?
För att få en uppfattning om vad för rötter som finns och vilken du kan välja, så rita de tio enhetsrötterna i den komplexa enhetscirkeln. Det behöver inte vara exakt. (Enhetsrötterna är alltså de z sådana att zn = 1, här n = 10.)
Yngve skrev:Ett komplext tal motsvarar en bestämd punkt i det komplexa talplanet.
För att två komplexa tal ska vara lika med varandra så måste båda talen motsvara samma punkt i det komplexa talplanet.
För att de ska motsvara samma punkt så måste både real- och imaginärdelarna vara lika.
Om de komplexa talen är skrivna på rektangulär form så finns det bara ett sätt att representera en specifik punkt i det komplexa talplanet.
Men ett komplext tal skrivet på polär form anges med hjälp av absolutbelopp (avstånd från origo) och en riktning (kallas även argument och avser motursvinkel mot den positiva delen av realdelsaxeln).
Absolutbeloppet (dvs avståndet) går inte att skriva på olika sätt, men riktningen (som anges med hjälp av argumentet) går att skriva på oändligt många sätt eftersom de trigonometriska funktionerna som används har en periodicitet på radianer (360°).
Det betyder att: och är lika med varandra, dvs motsvarar samma komplexa tal, om:
- , där är ett heltal.
Dvs
- absolutbeloppen måste vara lika stora
- argumenten måste antingen vara lika eller skilja sig åt med ett helt antal "varv".
Var det svar på din fråga?
Denna uppgiften löstes genom att ta hänsyn till cosinus utrycken och absolubeloppen o de båa leden, varför struntar man i sinus utrycket?
AlexanderJansson skrev:
Denna uppgiften löstes genom att ta hänsyn till cosinus utrycken och absolubeloppen o de båa leden, varför struntar man i sinus utrycket?
Kan du länka till eller ladda upp en bild av den lösningen?
Yngve skrev:AlexanderJansson skrev:Denna uppgiften löstes genom att ta hänsyn till cosinus utrycken och absolubeloppen o de båa leden, varför struntar man i sinus utrycket?
Kan du länka till eller ladda upp en bild av den lösningen?
r^10(cos(10v)+i*sin(10v))=1*(cos(0)+i*sin(0))
där cos(10v)=cos(0)
de sätter cos lika med varandra från båda leden.
Så om du skulle lösa ekvationen , hur skulle du göra då?
Anledningen till att man tittar just på cosinus och inte på sinus är att man skulle få för många lösningar då.
AlexanderJansson skrev:
r^10(cos(10v)+i*sin(10v))=1*(cos(0)+i*sin(0))
där cos(10v)=cos(0)
Den ekvationen är inte fullständig eftersom den endast ger en lösning, nämligen r = 1 och v = 0, dvs z = 1*(cos(0)+i*sin(0)), dvs z = 1.
Det är inte vad som efterfrågas.
Korrekt vore att istället sätta upp ekvationen
Lösningsmängden blir
- , dvs
Välj nu ett värde på som gör att så får du en icke-reell lösning.




