Fibonaccis talföljd och kalkylark
Hej! jag har en uppgift i flera steg. Den började med att man skulle göra ett kalkylark för fibonaccis talföljd. Fibonaccis talföljd är ju den där alla tal är summan av de två talen innan, förutomd e första 2 ettrona:
1, 1, 2, 3, 5...
jag lyckades med den delen. Sedan kom denna uppgift:
använda kalkylbladet som du skapade för fibonaccis talföljd. Bestäm i kolumn C kvoten av två på varandra följande tal i talföljden som du har beräknat i kolumn b. Vad händer med kvoten när n ökar?
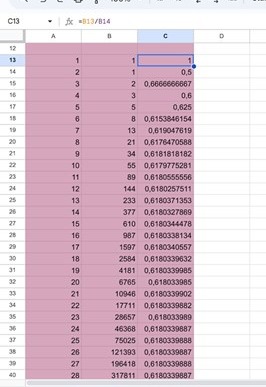
jag gjorde då såhär:
dock ska svaret vara att talen kommer närmre och närmre och närmre 1,6180.... vilket min inte gör. Då provade jag att göra tvärt om, alltså B14/B13. Men hur kunde jag vetat ordningen rätt från början genom att läsa frågan? Tycker inte den gör det så tydligt, så vill jättegärna ha några tips om jag missar något!
tack i förhand!
Jag tycker också att frågan är oklart formulerad. Den naturliga tolkningen är att du tar rad n / rad (n+1).
Men var det inte det som åsyftades? Din kvot kommer att gå mot 1/1,618…, men det är också ett fint tal.
Ditt tal är lösningen till ekv x2–x–1 = 0. Men ekvationen har två rötter (1±sqr5) / 2. Om du väljer plustecken får du 1, 618… . Väljer du minustecken får du roten –0,618…, som är just
–1/1,618… Och kvoten du räknar fram är just 0,618…
Det är sådana samband som har gjort att fibonacciföljden är så intressant.

