fel intgr.
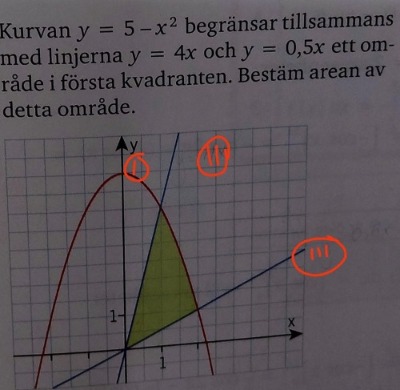
Jag ville ta (1) - (2) med integrationsgränserna 0 respektive 1.
Sedan ville jag addera ˆ ovan, med en integral (2) - (3) med integrationsgränserna 1 resp 2.
Detta är fel, kan någon förklara varför?
Rita integrationsgränserna så kommer du nog se varför det blir fel.
Tillägg: 2 nov 2023 23:25
Jag skulle integrerat andragradaren från 0 till , men då får jag 2 områden som jag sedan måste ta bort. Kan hitta ett sätt att ta bort de på?
Soderstrom skrev:Rita integrationsgränserna så kommer du nog se varför det blir fel.
Har inte så bra koll på hur man gör det på miniräknare? (När det gäller flera kurvor)
Smart.
De man vill få bort är de vita områdena,
kan man göra så? :
(1) - (2) med integrationsgränserna 0 respektive 1.
(3) med integrationsgränserna 0 till 2
Kör på det.
Edit: beräkningar för (3) är kommer inte för hela området, dock!
Tillägg: 3 nov 2023 00:15
Går bra att ta integrera sä: ((1)-(3)-(1)-(2))
Då får du gröna området.
Hur kommer du fram till det?
Din sista metod funkade och jag förstår nu den.
Men jag förstår inte varför den första metoden du föreslog inte funkar?
1. Först räknar man integralen av hela (1)
2. Sedan räknar man (1) - (2) med integrationsgränserna 0 och 1
3. Därefter räknar man (3) med integrationsgränserna 0 respektive 2,23. (((((Vad menar du med att "beräkningar för (3) är kommer inte för hela området".)))))
4. Sedan subtraherar man (totala) - (steg 2) - (steg 3)
naturnatur1 skrev:
Beteckningarna 1, 2 och 3 är förvirrande för mig eftersom de verkar stå för både funktioner/kurvor och områden.
Jag tolkar dina steg nedan med hjälp av beteckningarna A, B och C för de tre områdena, se bild.

Men jag förstår inte varför den första metoden du föreslog inte funkar?
1. Först räknar man integralen av hela (1)
Jag tolkar det som att integrera från 0 till . Det ger oss i så fall den sammanlagda arean av område A, B och C.
2. Sedan räknar man (1) - (2) med integrationsgränserna 0 och 1
Jag tolkar det som att integrera (5-x^2)-(4x) från 0 till 1. Det ger oss i så fall arean av område A.
3. Därefter räknar man (3) med integrationsgränserna 0 respektive 2,23. (((((Vad menar du med att "beräkningar för (3) är kommer inte för hela området".)))))
Jag tolkar det som att integrera 0,5x från 0 till . Det ger oss i så fall arean av område C.
4. Sedan subtraherar man (totala) - (steg 2) - (steg 3)
Jag tolkar det som (sammanlagda arean av A, B och C) - (arean av A) - (arean av C). Det ger oss I så fall arean av område B, vilket vi var ute efter.
Så den metoden fungerar utmärkt.
naturnatur1 skrev:(((((Vad menar du med att "beräkningar för (3) är kommer inte för hela området".)))))
Du skrev i svar #4
(3) med integrationsgrönserna 0 till 2
I så fall får du endast arean av det streckade området och den lilla biten från x =.2 till x = saknas då:

Då är jag med! Det konstiga är att jag fick fel när jag gjorde så som #7, antagligen jag som räknat fel då, ska räkna om.
Tillägg: 3 nov 2023 16:33
Det blev rätt. Tack!



