Feedback
Hej,
Frågan lyder
I vilken punkt på kurvan
y=x2−x
x2= x upphöjt till 2
är tangenten parallell med räta linjen
2x+3y−5=0
Man söker först k-värdet då dm har samma lutning i denna punkt o då får jag på/av den räta linjen (2x+3y-5) k=-2/3 (-0,67)
Sedan tog jag y prim (x)= 2x-1 (blir det 1 kvar a x:et?)
Söker y prim (x)= -2/3 (-0,67)
som blir 2x-1= -2/3
x= 0,17 (?)
Sätt in i funktion y (x)= x upphöjt till 2-x
y(0,17)= 0,17 upphöjt till 2-0,17= -0,1411
Svar: i punkten/erna (0,17, -0,14)
Känns spontant fel, gör jag något rätt,.:)?
Mvh/H
varför tycker du det är fel?
Hej,
Jag tycker inget, då jag inte har fokusert på detta, men har inlämning så försöker få det rätt...)
Så jag tänker alltså rätt, får jag det till rätt svar i punkten 0,17, -0,14 och om så vad säger dena punkt?
Enligt grafen med kurvan och tanget som du gjort så vad får man ut av den,vad ser man,tolkning?
Förstår inte riktigt på vilen punkt av kurvan, dvs en blåa, är tangenten, den gröna, parallell med räta linjen?
Jag har ju räknat ut ett svar men bra att förstå/tolka det också utifrån grafen som du nu gjort.
Mvh/H
Vilken
dvs den blåa
dena=denna
Stavar som en kratta..
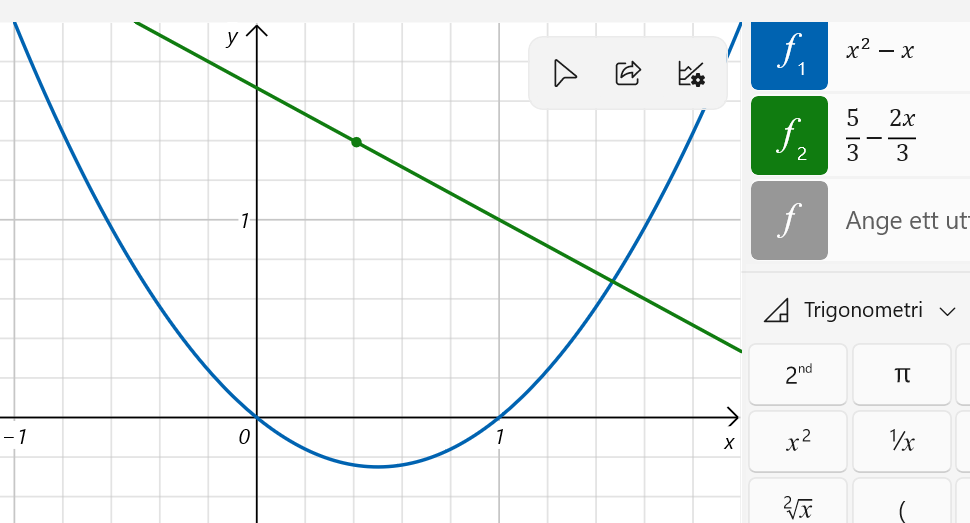
Bilden jag la in i #2 visar de två givna linjerna,
Om man tänker sig att du parallellförflyttar den gröna linjen till dess att den tangerar den blå så ser du att ditt svar är rimligt, du hamnar på ungefär (0,15;-0,12) dvs i stort sett samma som du räknade fram.
När man löser uppgifter brukar man svara med exakta värden om inget annat anges, du har svarat med närmevärden.
x blir i så fall 1/6 och y -5/36
Tack, ja, man kanske måste ha det i bråkform för att få det mer exakt och inte närmevärden, tack.
Aha, så hypotetiskt så flyttar man den parallellt ner mot den blåa kurvan och då blir det dessa punkter, i see/hear.
Mvh/Henning


