"Farligt fall" gränsvärde
Hej,
Jag har totalfastnat på följande:
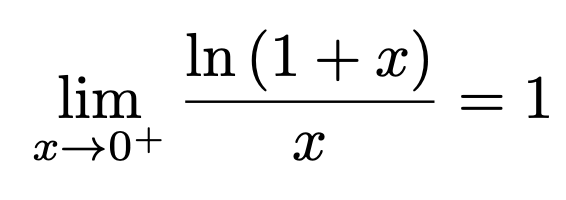
Jag förstår inte hur svaret kan bli 1 här. När x går mot 0 (från höger) så kommer täljaren typ bli ln(1) = 0, medan nämaren också närmar sig 0. Man kan tänka sig "0 / 0", vilket i mina ögon är ett så kallat farligt fall där man måste vara försiktig. Men varför blir det 1 här? Absolut att jag vet att svaret alltid blir 1 när man delar två likadana tal med varandra. I mitt fall närmar sig ju både nämnare och täljare 0, men jag har så svårt att greppa varför det skulle leda till att svaret blir 1? Tack på förhand.
Extra: kan inte heller förstå denna uppgift, som är i princip samma: ...som ska vara lika med:
...som ska vara lika med:

Var kommer tvåan ifrån? Jag förstår att om man förlänger täljaren med 2 och även nämnaren så har man inte förändrat uttrycket. Men då hade jag väl lika väl kunnat förlänga med vilket reelt tal som helst och sen skrivit att svaret är lika med det jag förlängde med?
den första är ett, som såvitt jag kommer ihåg, vanligt förekommande gränsvärde som vi lärde oss mer eller mindre utantill.
Annars ser man med hjälp av Taylorutveckling att det blir 1
Den andra, vitsen med att förlänga med 2 är att få samma faktor i nämnaren som du har i ln uttrycket.
Sen återför man lätt till det första gränsvärdet genom att substituera 2x = t varvid du får
2*(ln(1+t)/t) och t går mot 0+
Ture skrev:den första är ett, som såvitt jag kommer ihåg, vanligt förekommande gränsvärde som vi lärde oss mer eller mindre utantill.
Annars ser man med hjälp av Taylorutveckling att det blir 1
Den andra, vitsen med att förlänga med 2 är att få samma faktor i nämnaren som du har i ln uttrycket.
Sen återför man lätt till det första gränsvärdet genom att substituera 2x = t varvid du får
2*(ln(1+t)/t) och t går mot 0+
Tack för ditt svar Ture! Jag är lite osäker på vad Taylorutveckling är. Vad innebär det?
Läs om Taylorserie på wikipedia, en bit ner finns några exempel, bl.a ln(1+x)
Jag rekommenderar inte gärna l’Hôpital, för då riskerar man att döda all förståelse för gränsvärden, men kanske den regeln ar avsedd här.
Hej, då du inte hört talas om Taylorutveckling så kan jag visa. Så här gör du med Taylorutvecklingen.
Vi vet att våran funktion kan skrivas som en taylorserie, närmare bestämt att
, där är funktionen vi vill utveckla och är punkten vi vill utveckla kring! ( är den n:te derivatan av )
Vi är intresserade av en funktion som lite mer generellt uttryckt är , kring punkten 0 (detta resulterar i något som kallas maclaurin utveckling, ett specialfall av taylorutvecklingen!).
Deriverar vi får vi ,vi gör det för 3 termer(detta är mer än tillräckligt, du ser snart!). Deriveringen anser jag grundläggande, så den bör du kunna genomföra själv.
Sätter vi in i Taylorserien får vi
Vi har att vilket ger oss att
Det vi har nu är alltså att
Sätter vi in det i vårt ursprungliga uttryck har vi
Vi ser nu att alla x-termer blir 0, och gränsvärdet blir a. Vi kan dra 2 slutsatser utifrån detta.
- .
- .
Hoppas jag inte förvirrade dig!


