Får jag fram svaret genom att veta vad det 2 vinklarna "betyder" för varandra?
Hej,
En till vinkel uppgift som inte går för mig. Har prövat att räkna fram svaret genom att förstå placeringen av vinklarna och på de viset få fram ett värde på den vinkeln som söks.
Uppgiften är:
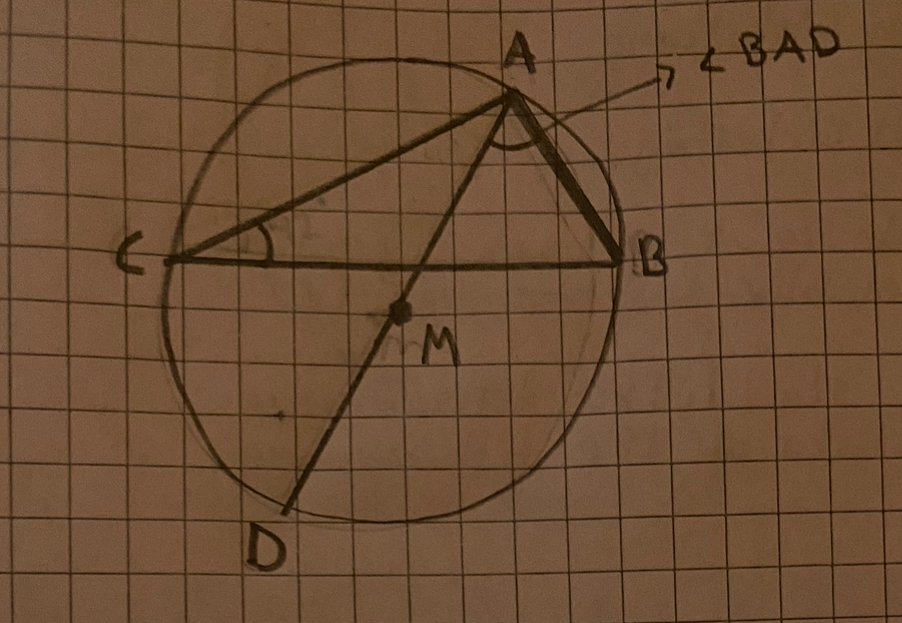
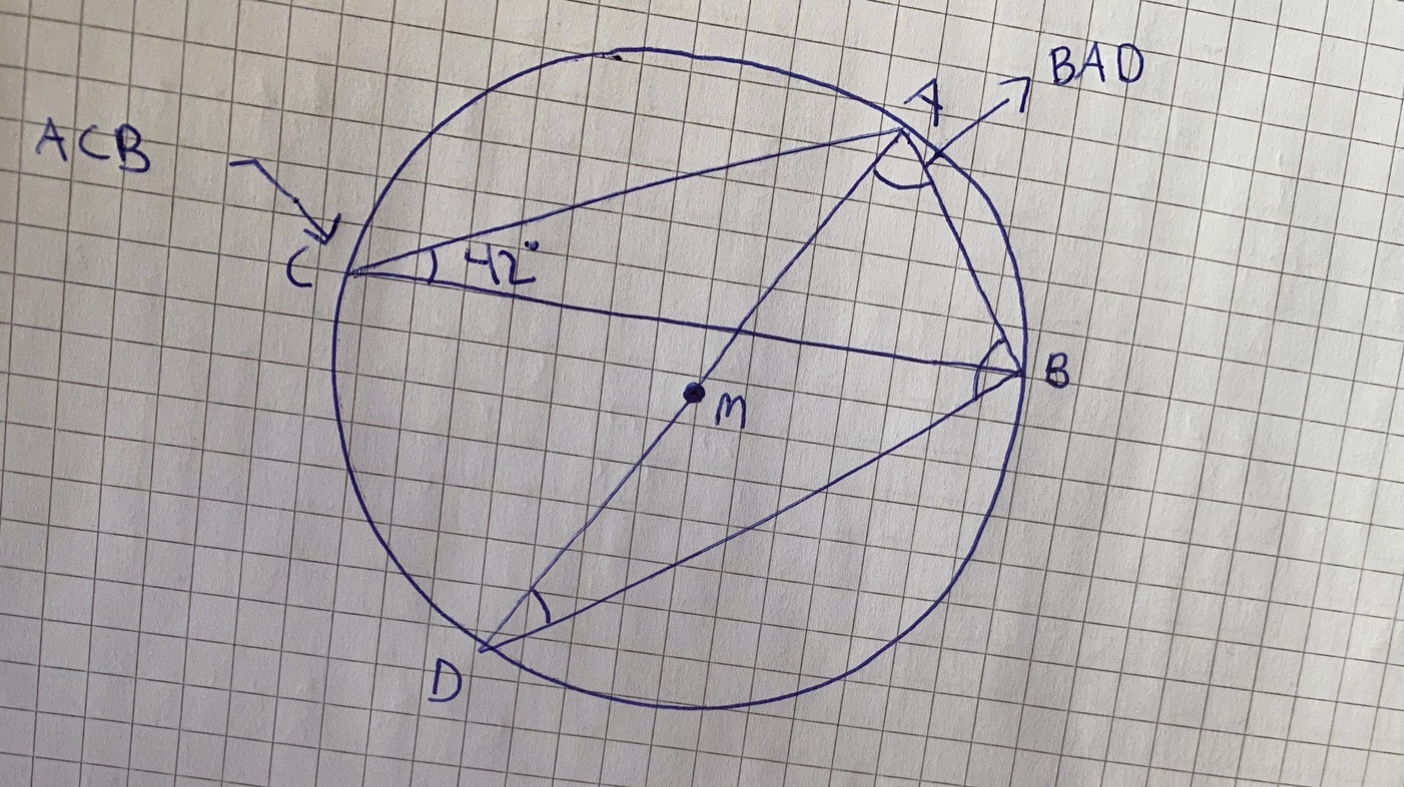
"Triangeln ABC är inskriven i en cirkel. ∠ACB = 42°. Rita av figuren och dra diametern AD. Hur stor är ∠BAD?"
Jag skickar en bild nedan på hur jag rita upp det hela och hoppas jag gjort rätt.
Jag har försökt lösa uppgiften genom att se placeringen på: ∠BAD till ∠ACB = 42°.
Det närmsta jag kommer svaret i facit är att tänka så här:
att vinklarna är alternatvinklar och alternatvinklar är ju lika stora, så då borde BAD vara 42 grader som ACB. Men det svaret är fel. Facit vill ha 48 grader och jag förstår faktiskt inte hur dom får fram det, hur gör man/tänker man här? 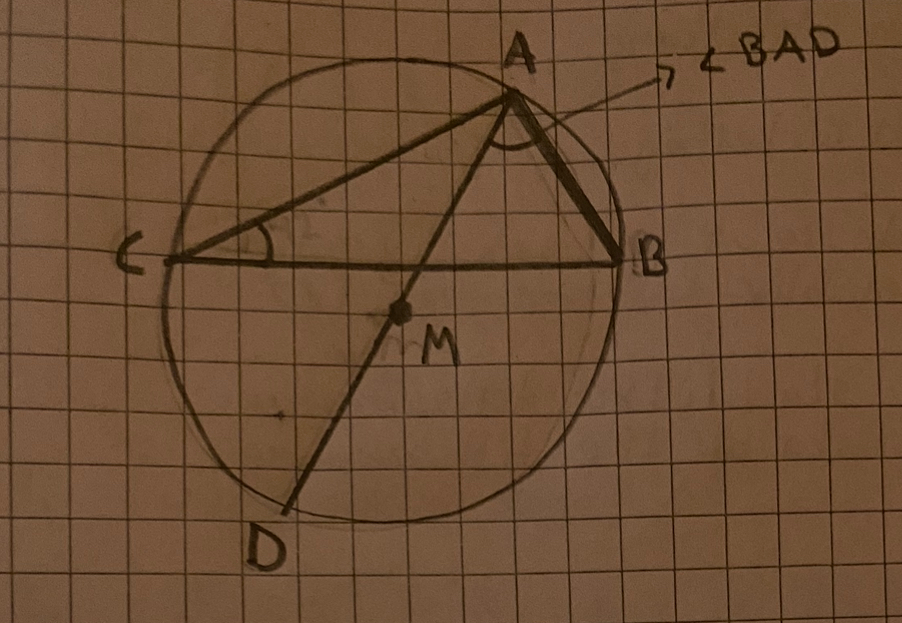
Naturens skrev:Hej,
En till vinkel uppgift som inte går för mig. Har prövat att räkna fram svaret genom att förstå placeringen av vinklarna och på de viset få fram ett värde på den vinkeln som söks.
Uppgiften är:
"Triangeln ABC är inskriven i en cirkel. ∠ACB = 42°. Rita av figuren och dra diametern AD. Hur stor är ∠BAD?"
Jag skickar en bild nedan på hur jag rita upp det hela och hoppas jag gjort rätt.
Jag har försökt lösa uppgiften genom att se placeringen på: ∠BAD till ∠ACB = 42°.
Det närmsta jag kommer svaret i facit är att tänka så här:
att vinklarna är alternatvinklar och alternatvinklar är ju lika stora, så då borde BAD vara 42 grader som ACB. Men det svaret är fel. Facit vill ha 48 grader och jag förstår faktiskt inte hur dom får fram det, hur gör man/tänker man här?
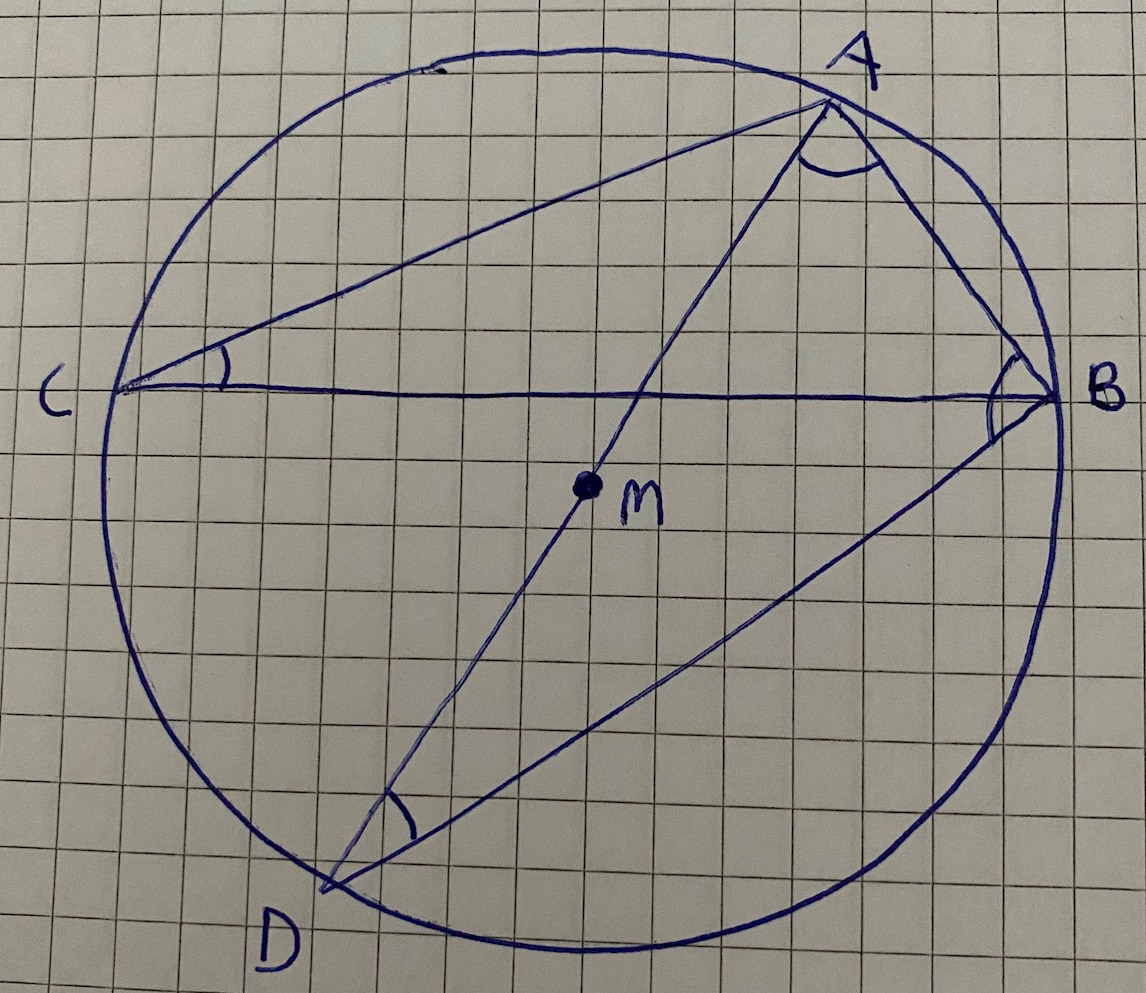
Dra linjen BD. Hur stor är vinkeln ADB? Hur stor är vi keln DBA? Hur stor är vinkeln BAD?
Det kan väl inte vara en rät, alltså 90 graders vinkel?
Det enda jag kan komma på är 180/3 men det känns fel?
Rita bilden och lägg upp den. Vilken vinkel är det du menar skulle vara rät, ADB, DBA eller BAD?
Här är en bild av en medelpunktsvinkel (svart) och en massa randvinklar på samma båge.

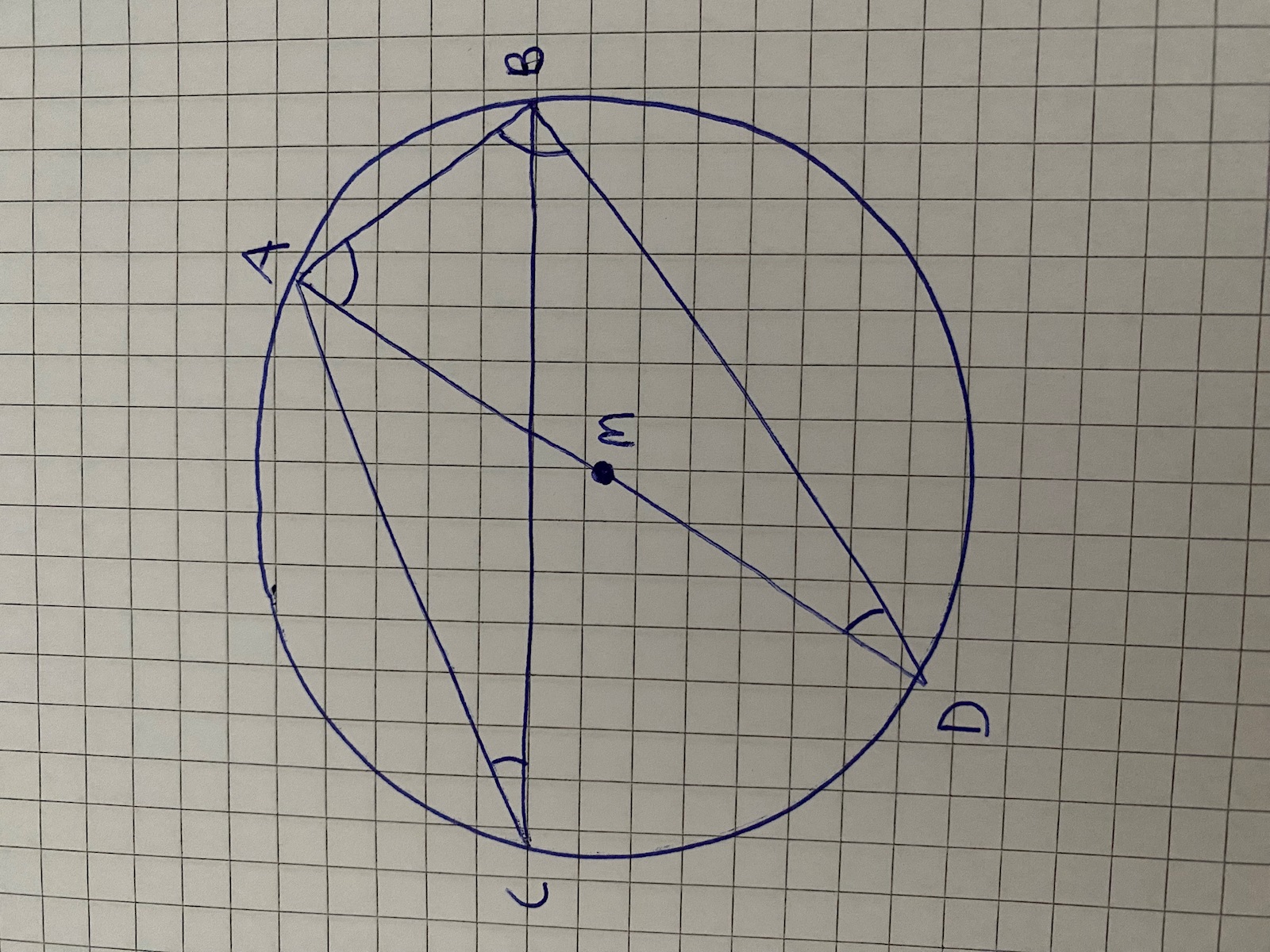
Hur ska man kunna veta vad vinklarna är när det ser ut så här, dvs jag har ingen grad på m så det jag har att gå på är vad det är för typ av vinklar och att det är en triangel och jag vet att den ska ha vinklar som är tillsammans 180 grader?
Har du sett det här? https://www.matteboken.se/lektioner/matte-2/logik-och-geometri/randvinkelsatsen#!/
Naturens skrev:
Hur ska man kunna veta vad vinklarna är när det ser ut så här, dvs jag har ingen grad på m så det jag har att gå på är vad det är för typ av vinklar och att det är en triangel och jag vet att den ska ha vinklar som är tillsammans 180 grader?
Ser du att vinkeln BDA är randvinkel på samma båge som vinkeln BCA? Hur stor är vinkeln BDA?
Ja jag ser att BDA är på samma båge som BCA? och ja jag har läst den där länken men vissa av dessa uppgifter förvirrar mig. Har svårt att se hur jag ska tolka figuren och hur jag ska lösa uppgiften, det har ju 4 hörn exempelvis. A B C och D är det då inte en fyrhörning exempelvis? och då vet jag ju att motsatt hörn ska tillsammans bli 180 grader, men det blir fel. Så jag vet inte hur jag ska kunna se figuren och veta hur jag ska kunna lösa uppgiften.
Det jag ser är att vinklarna BDA och BCA är på samma båge.
och sedan tittar jag på vinklarna liksom för att se om de kan ge mig någon information att gå på?
**
sen är det ju fler trianglar i en just på denna figur iallafall, finns ju 3 stycken och kan skapas fler så ja, jag är förvirrad just här och vet inte vad jag ska titta efter liksom..
Eftersom BDA och BCA är två randvinklar som är vönda mot mot/öppnar sig mot samma del av cirkelns rand så måste dessa två vinklar vara lika stora.
Uppgiften säger,
Triangeln ABC är inskriven i en cirkel.
Vinkeln ACB är 42 grader. (alltså vinkeln c på bilden jag rita)
Hur stor är vinkeln BAD. (vinkeln D på bilden jag rita)
om BDA och BCA är två randvinklar som är vända mot samma del av cirkelns rand och de två randvinklarna då måste vara lika stora så betyder de då inte att BAD också ska vara 42 grader?
Det var det jag skrev i början men facit vill ha 48 grader och jag bara inte förstår hur?
Vilken vinkel i triangeln ABD är det som är 42o? Vilken vinkel är det man frågar efter?
Typ här:
Du svarade inte på mina frågor. Är den här bilden klargörande?

Där D finns, där är det 42 grader ? i triangeln ABD.
Uppgiften frågar efter vinkeln jag skrev i bilden ?
**
Bilden du skicka med grönt och rött vet jag inte vad de ska visa.. det är alltså vinkeln BAD som uppgiften vill att jag lösa.
Båda de röda vinklarna är randvinklar på samma båge, så de är lika stora. Hur stor är vinkeln vid D?
De båda gröna vinklarna är medelpunktsvinkel (diametern) respektive randvinkel på samma båge. Hur stor är den gröna vinkeln vid B?
Använd vinkelsumman för en triangel för att räkna ut vinkeln BAD.
Okej, så vinkel D= 42 grader,
Vinkel B är en del av 180 grader, men är osäker på hur stor den vinkeln är.
men om C är 42 och D är 42 så är medelpunktsvinkeln 84 grader. För det är ju m=2r
Sen tänkte jag att om D är 42 och triangeln ska vara 180 grader att jag tar 180-42 svaret / på 2, men det blir fel.
Om jag vet m och r dvs m =2r, hur får jag reda på de andra vinklarna i respektive triangel ? jag har ju kollat vinklarna dvs vinkeln D till vinkeln B och hur dom sitter till förhållande till varandra & jag tycker dom står placerade så som dom sk för att ha samma storlek, men de blir fel
Du vet att diametern motsvarar en medelpunktsvinkel på 180o och att alla randvinklar är hälften så stora som motsvarande medelpunktsvinkel. Hur stor är allstå vinkeln ABD?
så...
Diametern från A till D är ju samma sak som en medelpunktsvinkel.
Och medelpunktsvinklar är diametern.
Diametern är dubbelt så stor som randvinkeln.
Randvinkeln har jag 2 av, båda är 42 grader.
Detta måste då betyda att diametern är 84 grader.
Den randvinkeln som "tillhör" den ritade diametern/medelpunktsvinkeln är 42 grader.
Randvinkeln och diametern/medelpunktsvinkeln skapar en "ny" triangel.
Eftersom att medelpunktsvinkeln (från A till D) utgör en sida av den "nya" triangeln.
Och alla vinklar på en triangel tillsammans blir 180 grader.
Så borde denna "nya" triangel även den ha vinklar som är 180 grader ihop.
MEN jag vet att randvinkeln är hälften så stor som motsvarande medelpunktsvinkel borde det då inte vara,
randvinkeln 42 grader, diametern då 84 grader?
och inte 180/2 = 90. 90-42 =48 ?
Jag vet att jag redan har randvinkeln D som är 42 grader.
Men vill veta vad det andra vinklarna är på den "nya" triangeln.
Tar jag 180 grader (alla vinklar i en triangel) och delar det på 2 (hälften så stor som vilken vinkel? diametern som är 84 är hälften så stor som randvinkeln 42? varför tar jag delat på 2 här?) får jag 90 grader.
Jag vet att jag har 42 grader som randvinkeln är i den "nya" triangeln.
Jag har tagit 180 grader (som är alla vinklar i triangeln sammanlagt)
och dividerat med 2 (vet inte varför jag delar 180 på 2 när randvinkeln på 42 har en medelpunktsvinkel som är 84, dvs 84 /2 =42)
Får jag 90 grader ( vad är det jag har räknat ut här? och hur vart det så här)
Tar jag bort 42 från 90, får jag kvar 48 och svaret på vad vinkeln BAD är, men... vad är då B om BAD är 48 och D är 42.
Tänker typ:
180-48-42 = 90, vinkeln B = 90 grader?
Försöker bara förstå den sista biten så jag kan skriva en sammanfattning under uppgiften så jag kan öva mer på den här uppgiften och liknande.
Varför tar jag 180 /2 ? hur viste du att du skulle ta 180/2 när du har en randvinkel som är 42 och en diameter som är 84?
Vad får jag fram då B? och hur fick jag fram B? typ hur tänkte du?
Naturens skrev:så...
Diametern från A till D är ju samma sak som en medelpunktsvinkel.
Och medelpunktsvinklar är diametern.
Diametern är dubbelt så stor som randvinkeln.
Randvinkeln har jag 2 av, båda är 42 grader.
Detta måste då betyda att diametern är 84 grader.
Den randvinkeln som "tillhör" den ritade diametern/medelpunktsvinkeln är 42 grader.
Randvinkeln och diametern/medelpunktsvinkeln skapar en "ny" triangel.
Eftersom att medelpunktsvinkeln (från A till D) utgör en sida av den "nya" triangeln.
Och alla vinklar på en triangel tillsammans blir 180 grader.
Så borde denna "nya" triangel även den ha vinklar som är 180 grader ihop.
MEN jag vet att randvinkeln är hälften så stor som motsvarande medelpunktsvinkel borde det då inte vara,
randvinkeln 42 grader, diametern då 84 grader?
Diametern är en rät linje, även kallad en rak vinkel, d v s 180o. Vinkeln ABD är hälften så stor, d v s 90o.
och inte 180/2 = 90. 90-42 =48 ?
Jag vet att jag redan har randvinkeln D som är 42 grader.
Men vill veta vad det andra vinklarna är på den "nya" triangeln.
Tar jag 180 grader (alla vinklar i en triangel) och delar det på 2 (hälften så stor som vilken vinkel? diametern som är 84 är hälften så stor som randvinkeln 42? varför tar jag delat på 2 här?) får jag 90 grader.
Jag vet att jag har 42 grader som randvinkeln är i den "nya" triangeln.
Jag har tagit 180 grader (som är alla vinklar i triangeln sammanlagt)
och dividerat med 2 (vet inte varför jag delar 180 på 2 när randvinkeln på 42 har en medelpunktsvinkel som är 84, dvs 84 /2 =42)
Får jag 90 grader ( vad är det jag har räknat ut här? och hur vart det så här)
Tar jag bort 42 från 90, får jag kvar 48 och svaret på vad vinkeln BAD är, men... vad är då B om BAD är 48 och D är 42.
Tänker typ:
180-48-42 = 90, vinkeln B = 90 grader?
Försöker bara förstå den sista biten så jag kan skriva en sammanfattning under uppgiften så jag kan öva mer på den här uppgiften och liknande.
Varför tar jag 180 /2 ? hur viste du att du skulle ta 180/2 när du har en randvinkel som är 42 och en diameter som är 84?
Vad får jag fram då B? och hur fick jag fram B? typ hur tänkte du?
Du verkar röra ihop att 180o dels är en rät linje = ett halvt varv, dels ärvinkelsumman i en triangel.
Vinkeln ADB är 42o eftersom den är en randvinkel på samma båge som vinkeln ACB, som är 42o.
Vinkeln DBA är 90o eftersom den är randvinkel till en diameter.
Vinkeln ABD är 48o eftersom 180-90-42 = 48o (vinkelsumman i en triangel).
Hej, igen. Har läst dina svar och läst lite mer om randvinklar för att försöka förstå bättre.
Försökt sammanfatta det till 3 frågor typ:
1) Diametern från A-D är en medelpunktsvinkel/ en rät linje/ett halvt varv/ vinkelsumman av en triangel och där med 180 grader. Men samtidigt så står det att "Enligt randvinkelsatsen är medelpunktsvinkeln till en cirkelbåge dubbelt så stor som en randvinkel till samma båge." och om jag utgår från det, och utgår från randvinkeln jag har som är 42 grader, så betyder de ju att diametern ska vara 84grader, men den är också 180 grader för den är en rät linje och ett halvt varv osv, så frågan är, vilken grad är det jag ska utgå från, dvs nu vart det 180 grader för jag behöver veta en annan vinkels grad, men om frågan i uppgiften hade varit vad är det för grad på diametern vad hade jag då svarat? 84 antar jag då jag hade utgått från randvinkeln men är det fel ska det vara 180 liksom?
2) Tror jag har svårast för denna del. När det kommer till vinkeln DBA så läste jag någonstans att " i en halvcirkel är medelpunktsvinkeln 180 grader och randvinkeln är hälften". Den enda medelpunktsvinkeln jag kan se i denna uppgift är den jag rita in, och eftersom att den är medelpunktsvinkeln och skapar då en halv cirkel, så ska randvinkeln till den vara 90grader. Är det då den randvinkeln som inte är "kopplad" till den medelpunktsvinkeln som blir 90 grader? dvs DBA, detta då både ADB och BAD är "en del av vinkeln" kan jag se de så i kommande uppgifter? att det liksom är den vinkeln som inte "sitter fast" med medelpunktsvinkeln som är hälften så stor som 180 grader? och inte dom andra? och om jag då exempelvis har 2 vinklar mitt emot medelpunktsvinkeln då betyder de då att det båda är hälften så stor som medelpunktsvinkeln dvs 180 grader?
3)Jag har tänkt en del också på hur jag enklast kan komma ihåg hur man räknar ut sånt här. Och jag vet inte om det här tänket är "bra" men tänkte ändå skriva till dig hur jag liksom tänker lite kring uträkningen:
Om jag vet att jag har en randvinkel som är 42 grader, då den är på samma cirkelbåge som en annan randvinkel med samma grad.
Och jag vet att randvinkeln mitt emot medelpunktsvinkeln är 90 grader
så bara adderar jag ihop dom = 132
sen tar jag 132 - 180 och får den tredje och okända vinklens grad dvs 48?
Naturens skrev:[...]
1) Diametern från A-D är en medelpunktsvinkel/ en rät linje/ett halvt varv/ vinkelsumman av en triangel och där med 180 grader.
Du blandar ihop begreppen här.
En diameter (AD) är ett linjesegment, nte en vinkel, inte heller en vinkelsumma av en triangel. Du kan alltså inte säga att en diametern är 180°, inte heller att en diameter är en vinkelsumma av en triangel.
Den medelpunktsvinkel som du avser kan vi kalla vinkeln AMD. Denna medelpunktsvinkel är mycket riktigt 180°
Men samtidigt så står det att "Enligt randvinkelsatsen är medelpunktsvinkeln till en cirkelbåge dubbelt så stor som en randvinkel till samma båge." och om jag utgår från det, och utgår från randvinkeln jag har som är 42 grader, så betyder de ju att diametern ska vara 84grader, men den är också 180 grader för den är en rät linje och ett halvt varv osv, så frågan är, vilken grad är det jag ska utgå från, dvs nu vart det 180 grader för jag behöver veta en annan vinkels grad, men om frågan i uppgiften hade varit vad är det för grad på diametern vad hade jag då svarat? 84 antar jag då jag hade utgått från randvinkeln men är det fel ska det vara 180 liksom?
Vinkeln ACB (42°) är inte en randvinkel till medelpunktsvinkeln AMB, efrersom de inte "är vända mot"/"öppnar sig mot" samma del av cirkelns rand.
I bilden, där jag har ritat in radien MB, ser du att ACB är randvinkel till AMB. Detta eftersom de "är vända mot"/"öppnar sig mot" samma del av cirkelns rand (det blåmarkerade).

Naturens skrev:[...]
2) Tror jag har svårast för denna del. När det kommer till vinkeln DBA så läste jag någonstans att " i en halvcirkel är medelpunktsvinkeln 180 grader och randvinkeln är hälften". Den enda medelpunktsvinkeln jag kan se i denna uppgift är den jag rita in, och eftersom att den är medelpunktsvinkeln och skapar då en halv cirkel, så ska randvinkeln till den vara 90grader. Är det då den randvinkeln som inte är "kopplad" till den medelpunktsvinkeln som blir 90 grader? dvs DBA, detta då både ADB och BAD är "en del av vinkeln" kan jag se de så i kommande uppgifter? att det liksom är den vinkeln som inte "sitter fast" med medelpunktsvinkeln som är hälften så stor som 180 grader? och inte dom andra? och om jag då exempelvis har 2 vinklar mitt emot medelpunktsvinkeln då betyder de då att det båda är hälften så stor som medelpunktsvinkeln dvs 180 grader?
Jag förstår inte vad du menar med att "... ADB och BAD är en del av vinkeln".
Jag förstår inte heller din fråga som rör vinklar som inte "sitta fast" med medelpunktsvinkeln eller "mitt emot" medelpunktsvinkeln.
Kan du visa med ett exempel?
======
Men det stämmer att en randvinkel som hör ihop med medelpunktsvinkeln AMD är vinkeln DBA. Detta eftersom dessa båda vinklar "är vända mot"/"öppnar sig mot" samma del av cirkelns rand, dvs mot samma cirkelbåge, blåmarkerad i bilden.
Är du med på att det betyder att vinkeln DBA är 90°?

Naturens skrev:[...]
3)Jag har tänkt en del också på hur jag enklast kan komma ihåg hur man räknar ut sånt här. Och jag vet inte om det här tänket är "bra" men tänkte ändå skriva till dig hur jag liksom tänker lite kring uträkningen:
Om jag vet att jag har en randvinkel som är 42 grader, då den är på samma cirkelbåge som en annan randvinkel med samma grad.
Och jag vet att randvinkeln mitt emot medelpunktsvinkeln är 90 grader
så bara adderar jag ihop dom = 132
sen tar jag 132 - 180 och får den tredje och okända vinklens grad dvs 48?
I den här uppgiften fungerar det tänket eftersom randvinkeln som är 90° befinner sig i samma triangel som randvinkeln som är 42°.
Men varje uppgift är unik så det är ingen idé att försöka använda genvägar liknande den du beskrev här.
Jätte tack för all hjälp, uppskattar det mycket. Har fått svar på mina frågor och jag hänger med mycket bättre nu. Får se hur det går i kommande uppgifter men förstår mycket mycket bättre nu. Tack för tålamodet.