Få fram x
Hej,
uppgiften är:
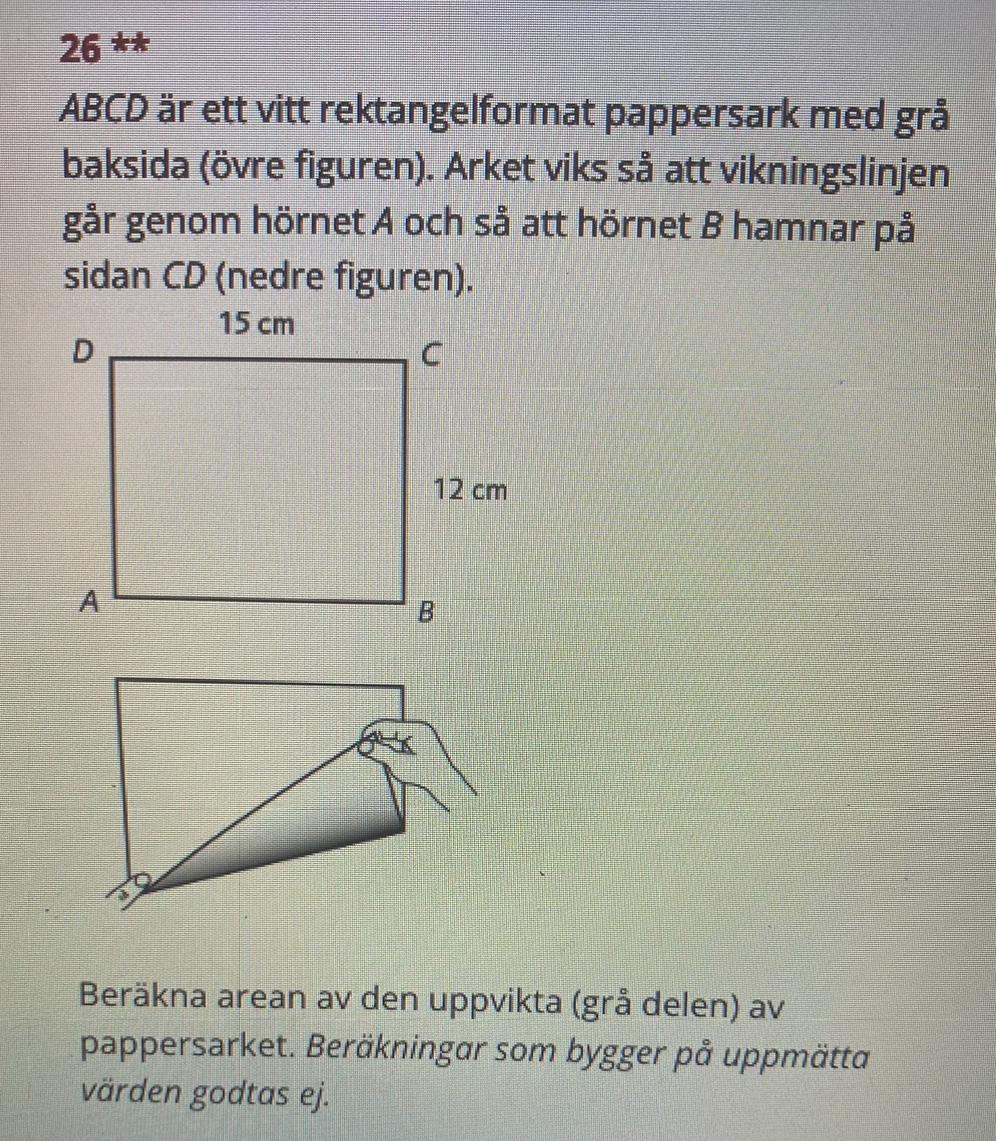jag har gjort så här:
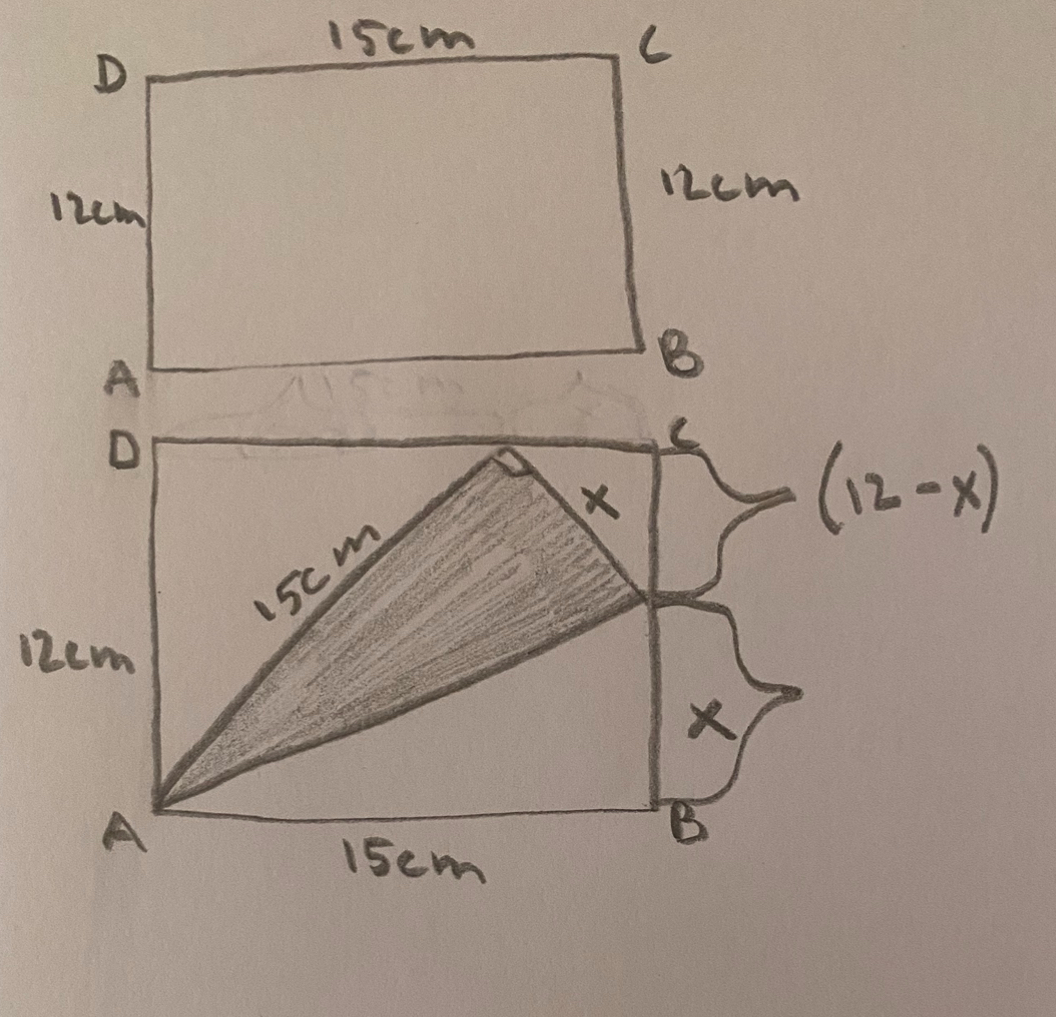
jag tänker att jag behöver veta höjden på triangeln dvs X för att kunna få fram arean.
först tänkte jag att jag kunde ta hjälp av Pythagoras sats, men blir osäker på hur det skulle se ut. Jag känner ju inte till 2 sidor på triangeln den ena sidan är 15 & den andra sidan är x? Så det blir svårt att använda Pythagoras då, jag har dock 12cm och 15cm i rektangeln så för att få fram x tänker jag väl att jag kanske kan sätta in rektangelns värden i satsen typ:
rektangeln:
höjd 12cm
höjd (12-x) sen x
bredd 15 cm
satsen:
a^2+ b^2=c^2
så typ
12^2 + (12-x)^2 =15^2 för att få fram x? Men de här känns fel?
Bra att du har ritat en figur! Jag kan dock inte "se" den triangeln du har ställt upp Pythagoras sats på. Det finns ingen triangel med katetrarna (12-x) och 12.
Du kan dock beräkna den lila och den gröna sidan med hjälp av Pythagoras sats och att du vet att hela långsidan är 15 cm.
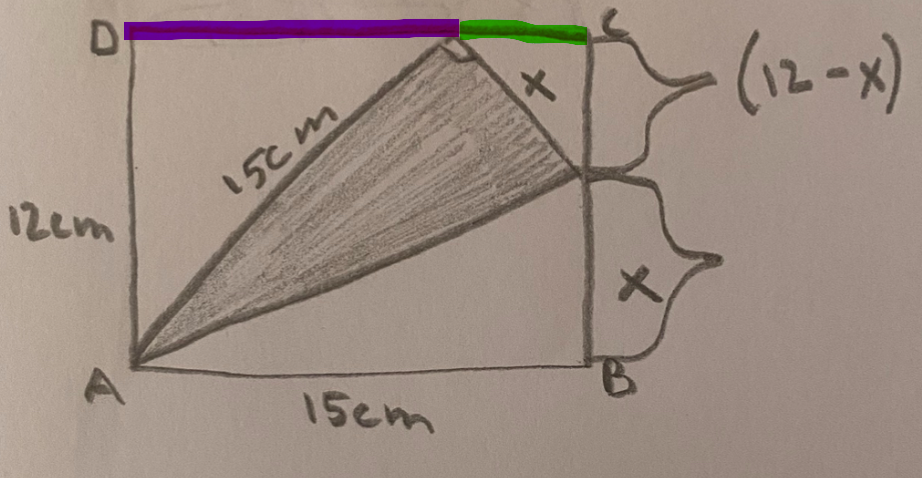
Hej, Okej men hur då?
jag la till (15-x) & x mellan DC
menar du att jag typ gör två stycken då?
alltså typ ser efter de vita trianglarna som skapas av den grå?
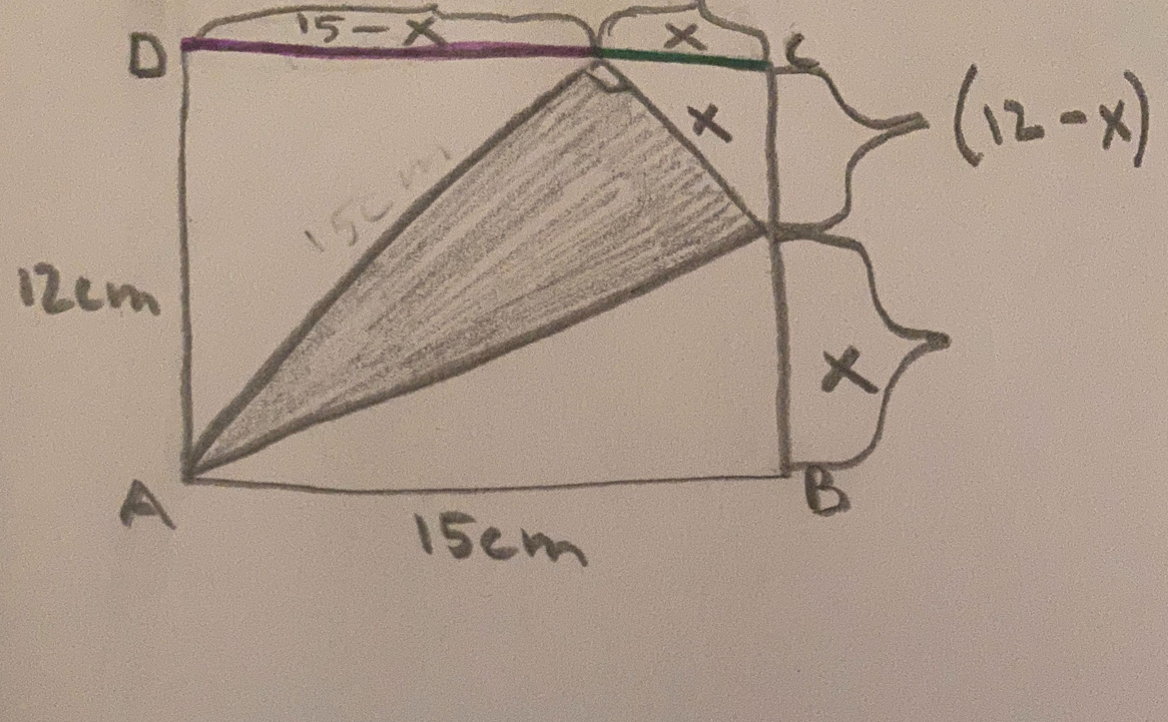
Var försiktig med hur du använder x. Du vet inte att den gröna delen har samma längd som det x mellan B och C. Det är bättre att använda en annan bokstav, även om det till en början gör att du får två okända. Kanske kan den lila sidan få heta y så kan du använda Pythagoras sats:
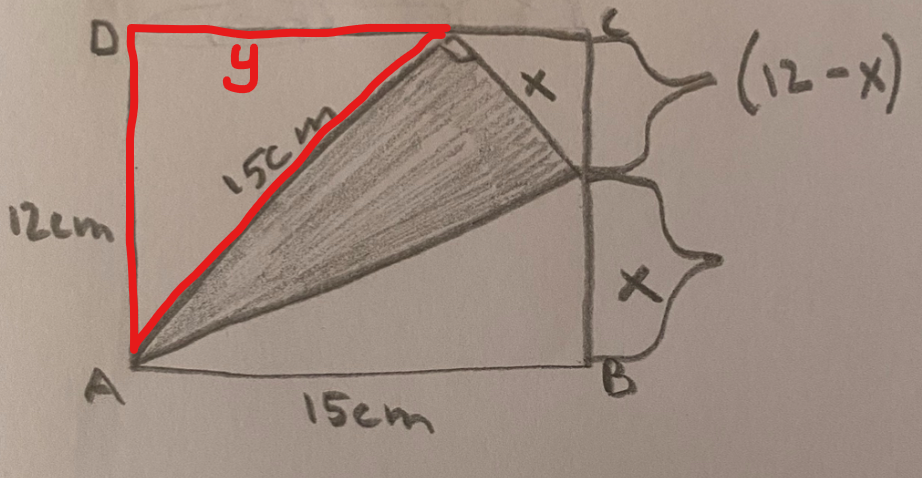
tack för tipset.
Jag fick y till 9 (lila)
och "grön" till 6
för att få fram höjden dvs x så antar jag att jag tar:
6^2 + (12-x)^2=c^2
& vidare det x värdet och 15 cm för att få fram arean?
***
jag fastnar när jag försöker räkna:
6^2+(12-x)^2=c^2 (det går inte)
Jag skriver här hur jag försöker räkna fram det:
a^2 + b^2 =c^2
6^2 + (12-x)^2 =x^2
36 + 144 - x^2 = x^2
180 -x^2=x^2
180 -x^2 +x^2= x^2 +x^2
180=x^2 + x^2 (det blir konstigt...)
(roten ur) 180 = (roten ur) x^2 + (roten ur) x^2 (det blir mer konstigt...)
Snyggt. Det kanske bara har blivit tokigt när du gjort beräkningarna för själva proceduren är rätt.
Ledtråd: Det blir fel när du utvecklar (12-x)2. Använd kvadreringsregeln.
men ojj! JÄTTE TACK! fick ut svaret rätt till slut. : )
En variant är att se att den röda triangeln i fners figur är likformig med triangeln med C som hörn.
När man bestämt att en katet i den senare triangeln är 6 cm är det enkelt att bestämma x (hälften av 15 cm).
smart grej, tack
