Extremvärden i R3 inom region
Hej, när jag undersöker extremvärdena på kvadraten, 0<=x<=1, 0<=y<=1 så får jag maxvärdet till 1. När jag kollar i geogebra så är maxvärdet 2. Vad gör jag för fel i mina beräkningar?
Maxvärdet fås då (x, y) = (1, 1).
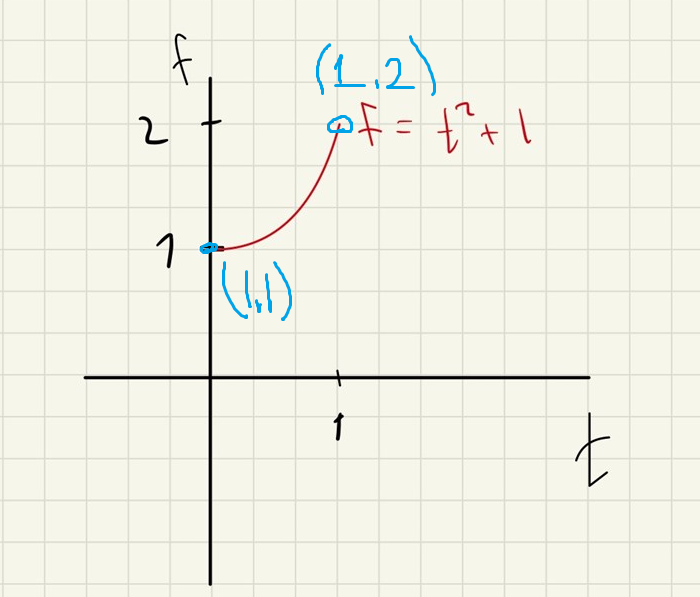
På linjen mellan (0, 1) och (1, 1) fick du f(t, 1) = t2 + 1 för 0 t 1. Hur ser denna funktion ut?

Tillägg: 1 sep 2022 23:04
Tänk på att x2 + y2 är avståndet (i kvardat) till origo från punkten (x, y). Vilken punkt (x, y) i området har störst avstånd till origo och vilken punkt har minst avstånd till origo?
PATENTERAMERA skrev:Maxvärdet fås då (x, y) = (1, 1).
På linjen mellan (0, 1) och (1, 1) fick du f(t, 1) = t2 + 1 för 0 t 1. Hur ser denna funktion ut?
Tillägg: 1 sep 2022 23:04
Tänk på att x2 + y2 är avståndet (i kvardat) till origo från punkten (x, y). Vilken punkt (x, y) i området har störst avstånd till origo och vilken punkt har minst avstånd till origo?
(2,1) har störst avstånd och (1,0) minst. Försöker inse vad som gick fel i mina beräkningar för det ska va rätt i alla fall när jag granskar linje 1) och 2).
(2, 1) ligger inte i området. Menar du kanske (1, 1)?
PATENTERAMERA skrev:(2, 1) ligger inte i området. Menar du kanske (1, 1)?
Edit: Självklart är den vänstra punkten (0,1)
OK. Men tänk på att y-värdet i grafen är funktionsvärdet f(t, 1) och inte y-koordinaten för en punkt (x, y) i definitionsområdet för f.
Grafen skall tolkas så att funktionen f, på linjen 2, har det minsta värdet 1 då t = 0, dvs i punkten (x,y) = (0, 1), och det största värdet 2 då t = 1, dvs i punktet (x, y) = (1, 1).
PATENTERAMERA skrev:OK. Men tänk på att y-värdet i grafen är funktionsvärdet f(t, 1) och inte y-koordinaten för en punkt (x, y) i definitionsområdet för f.
Grafen skall tolkas så att funktionen f, på linjen 2, har det minsta värdet 1 då t = 0, dvs i punkten (x,y) = (0, 1), och det största värdet 2 då t = 1, dvs i punktet (x, y) = (1, 1).
Tack! Borde inte linje 2 ge exakt samma värde då?
Det är linje 2 jag pratar om.
PATENTERAMERA skrev:Det är linje 2 jag pratar om.
Oj, trodde vi pratade om linje 3. Så här har min lärare löst linje 2 (https://www.youtube.com/watch?v=Y73iWwB_Nuk) och han får punkten (0,1), är det inte denna punkten vi ska stoppa in i f(x,y)=x2+y2. Skulle vilja parametrisera linje 3 på samma sätt, men får inte till det.
Han verkar missa den punkten. Men han har ändock med (1, 1) som en kandidat på slutet. Oklart hur han identifierade (1, 1) som kandidat. Men vi vet ju hur funktionen 1 + t2 ser ut, vi behöver inte derivera. Vi ser direkt att minsta värde ges då t = 0 och största värde då t = 1. Du bör inte bara titta på de punkter där derivatan är noll utan även på ändpunkterna. Här ges största värde i ändpunkten t = 1, men derivatan är ju inte noll där. Om du bara tittar på punkter med derivatan noll så missar du denna punkt. Vilket är tråkigt, eftersom det är där som maximum finns.
Linje 3 kan parametriseras som
x(t) = 1
y(t) = t
f(1, t) = 1 + t2
0 t 1.
Så du får liknande resonemang som på linje 2.
PATENTERAMERA skrev:Linje 3 kan parametriseras som
x(t) = 1
y(t) = t
f(1, t) = 1 + t2
0 t 1.
Så du får liknande resonemang som på linje 2.
Jag tänker som dig där ja, men om du lyssnar vid 3.48 så säger han att vi ska ta 1-t, han måste väl då mena
x(t)=1
y(t)=1-t
0≤t≤1
Vi får då
f(1,1-t)=1+1-2t+t2=f(t)
f'(t)=2t-2=0
t=1
Så
(x,y)=(1,0)
Vilket återigen ger maxvärdet f(1,0)=1 suuuuck
Edit: Det är väl absolut ingen skillnad på att kalla y(t)=t och y(t)=1-t när intervallet är 0≤t≤1
Det är samma typ av parametrisering. Han går från (1, 1) (t=0) till (1, 0) (t=1), vi går åt andra hållet. Men det är ju en smaksak. Notera att återigen är den punkt han får fram ett minimum på linjen. Du kan skriva om hans funktion som 1 + (t-1)2. Vi ser direkt att min sker då t = 1 (punkten (1, 0)) och max då t = 0 (punkten (1, 1)).
PATENTERAMERA skrev:Vi ser direkt att min sker då t = 1 (punkten (1, 0)) och max då t = 0 (punkten (1, 1)).
Förstår inte detta riktigt, hänvisar du till den grafen du ritade? där sker max vid t=1
Nej, detta är linjen 3 i din figur. Vår parmetrisering av linjen 3 går från nedre hörnet till det övre. Lärarens i motsatt rikning.
PATENTERAMERA skrev:Nej, detta är linjen 3 i din figur. Vår parmetrisering av linjen 3 går från nedre hörnet till det övre. Lärarens i motsatt rikning.
Så lärarens metod fungerar inte då? konstigt


