Exponentialfunktionens derivata
Jag har ingen ordning hur man löser denna uppgiften: Bestäm den punkt på funktionen 𝑔(𝑥) där 𝑔′(𝑥)=3. 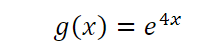
Titta I din formelsamling.
Där finns en deriveringsregel för ekx.
I fallet g(x) = e4x så är k = 4.
Ta ned hjälp av detta fram uttrycket för g'(x).
Sätt detta uttryck lika med 3 och lös ut x ur ekvationen.
g´(x)=4e4x
g´(3)=4e12
men är detta svaret?
Derivatan g'(x) = 4e4x är korrekt, men det är inte g'(3) som efterfrågas utan istället den punkt där g'(x) = 3 gäller.
4e4x=3 hur ska jag räkna det?
efter förenkling kan du använda naturliga logaritmen
4e4x=ln3
218x=1,1
x=1,1/218, x=5 är det rätt svar?
Nej, e4x är inte samma sak som e4·x
Om du börjar med att dela bägge led med 4, vad får du då?
Sedan tror jag att du hittar vad 4x är ganska lätt.
jag fattar inte riktigt vad man ska göra e4x=ln(3/4)?
Nej, nu har du logaritmerat det ena ledet men inte det andra.
e4x får du när du har delat med 4. Hoppa inte över det.
Hur blir det när du sedan tar logaritmen av vänster- och högerleden?
det kommer inte att funka med lne4x=ln(3/4)
4x=-0,287
x=-0287/4
x=-0,07
jag vet inte om detta är rätt?
Det är helt rätt.
tack så mycket för hjälpen =)



