Exakt värdena för cos v och tan v om sinv = -4/5

Du kan använda trigettan. Vet du vad det är?

mrpotatohead skrev:

Du kan använda trigettan. Vet du vad det är?

Trigonometriska ettan ingår inte i kursen Ma3c.

Uppgiften föreslår att man ska använda enhetscirkeln tolkar jag det som.

rita en rätvinklig triangel, förslagsvis med hypotenusan 1 och motstående katet 4/5. Då kan du räkna ut cosx om x=4/5. Försök sedan hitta samband mellan 4/5 och -4/5 i enhetscirkeln och hitta den/de värdena på cosv

wangster skrev:

rita en rätvinklig triangel, förslagsvis med hypotenusan 1 och motstående katet 4/5. Då kan du räkna ut cosx om x=4/5. Försök sedan hitta samband mellan 4/5 och -4/5 i enhetscirkeln och hitta den/de värdena på cosv

Funkar det?

Det lät som en spännande lösning jag aldrig provat. 

wangster skrev:

rita en rätvinklig triangel, förslagsvis med hypotenusan 1 och motstående katet 4/5. Då kan du räkna ut cosx om x=4/5. Försök sedan hitta samband mellan 4/5 och -4/5 i enhetscirkeln och hitta den/de värdena på cosv

Jag fattade inte riktigt.

Du komplicerar uppgiften onödigt mycket.

Framför dig har du en rätvinklig triangel med två kända sidor av tre.

Finns det något samband som du kan använda dig av för att få reda på den tredje?

Mesopotamia skrev:

Du komplicerar uppgiften onödigt mycket.

Framför dig har du en rätvinklig triangel med två kända sidor av tre.

Finns det något samband som du kan använda dig av för att få reda på den tredje?

Ledtråd

Pythagoras sats.

Men är triangeln jag ritade rätt?
I sånna fall blir det 
x= roten ur 1-0.16

Du har ritat rätt men räknat fel.

$$\begin{gathered} a^2+b^2=c^2 \\ 0,8^2+b^2=1^2 \\ {b}^2=1-0,64 \\ b=\pm \sqrt{0,36} \end{gathered}$$

negativ rot irrelevant eftersom sträcka är positiv.

b=0,6

Kommer du vidare?

Mesopotamia skrev:

Du har ritat rätt men räknat fel.

$$\begin{gathered} a^2+b^2=c^2 \\ 0,8^2+b^2=1^2 \\ {b}^2=1-0,64 \\ b=\pm \sqrt{0,36} \end{gathered}$$

negativ rot irrelevant eftersom sträcka är positiv.

b=0,6

Kommer du vidare?

Ok, nu ser jag. Och vinkeln blir då  0,8/1 =0.8  
sin-1 0.8= 53 grader

Det är förmodligen tänkt att du ska räkna exakt, använd en enklare triangel i fjärde kvadranten, t.ex. den här

Tillägg: 3 jan 2024 19:52

Fixade grafen, x-värdet 3 ska vara positivt

D4NIEL skrev:

Det är förmodligen tänkt att du ska räkna exakt, använd en enklare triangel i fjärde kvadranten, t.ex. den här

Hur fick du fram dom numrena?

När man ser $\sin(v)=4/5$ ska man genast tänka sig att motstående katet är 4 och att hypotenusan är 5, eftersom sinus definieras som motstående katet genom hypotenusan. Den enklaste rätvinkliga triangel som uppfyller detta är den med sidorna (3,4,5).

Vi får också veta att vinkeln ligger i fjärde kvadranten, där är x-värdena positiva och y-värdena negativa.

Fjärde kvadranten är vinklarna mellan -90 grader och 0 grader eller mellan 270 grader och 360 grader, hur man nu vill se på det. Det är viktigt att du kan identifiera vilken del av enhetscirkeln det gäller.

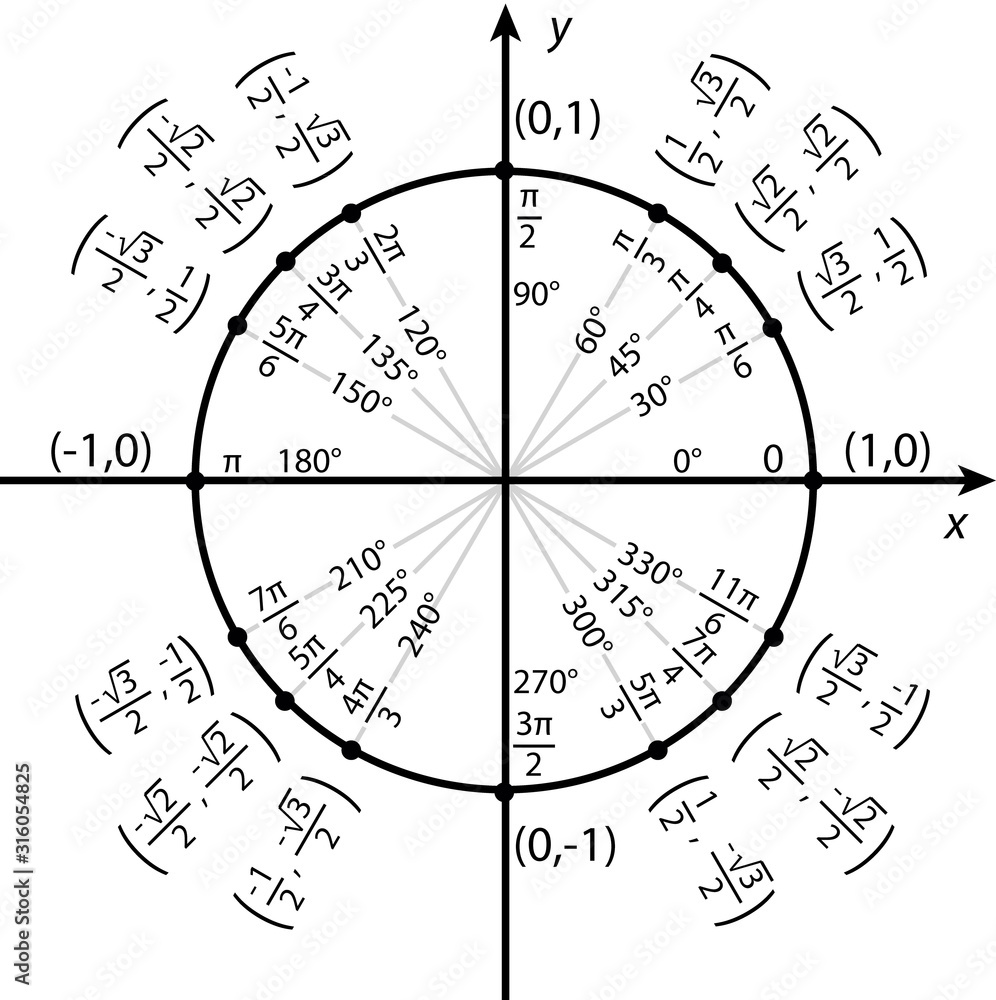
En triangel som uppfyller villkoren är

Notera att jag rättade grafen i mitt förra inlägg.

Från grafen framgår det att cos (närliggande katet delat med hypotenusan) blir $\frac 35$ samt att tan (motstående genom närliggande) blir $-\frac 43$

D4NIEL skrev:

När man ser $\sin(v)=4/5$ ska man genast tänka sig att motstående katet är 4 och att hypotenusan är 5, eftersom sinus definieras som motstående katet genom hypotenusan. Den enklaste rätvinkliga triangel som uppfyller detta är den med sidorna (3,4,5).

Vi får också veta att vinkeln ligger i fjärde kvadranten, där är x-värdena positiva och y-värdena negativa.

Fjärde kvadranten är vinklarna mellan -90 grader och 0 grader eller mellan 270 grader och 360 grader, hur man nu vill se på det. Det är viktigt att du kan identifiera vilken del av enhetscirkeln det gäller.

En triangel som uppfyller villkoren är

Notera att jag rättade grafen i mitt förra inlägg.

Från grafen framgår det att cos (närliggande katet delat med hypotenusan) blir $\frac 35$ samt att tan (motstående genom närliggande) blir $-\frac 43$

Tack så mycket för infon. Det är uppskattat.