Evaluera integral (igen)

Kan du använda att 

$\tan^3u=\tan u(\tan^2u+1)-\tan u$

?

Då får du en produkt av tan u och dess derivata. 

Såhär långt kommer jag, men sen fastnar jag igen

$\displaystyle \int \tan u(\tan^2u+1)du= \int t dt= \dfrac{t^2}{2}+C$

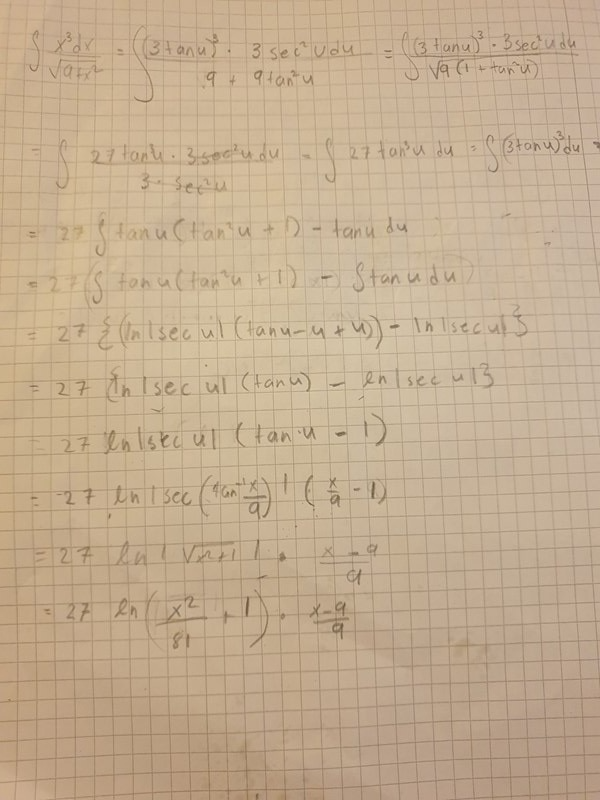
med t = tan(u), dt = (tan²u +1)du

såhär gör jag, men det blir fel igen :(

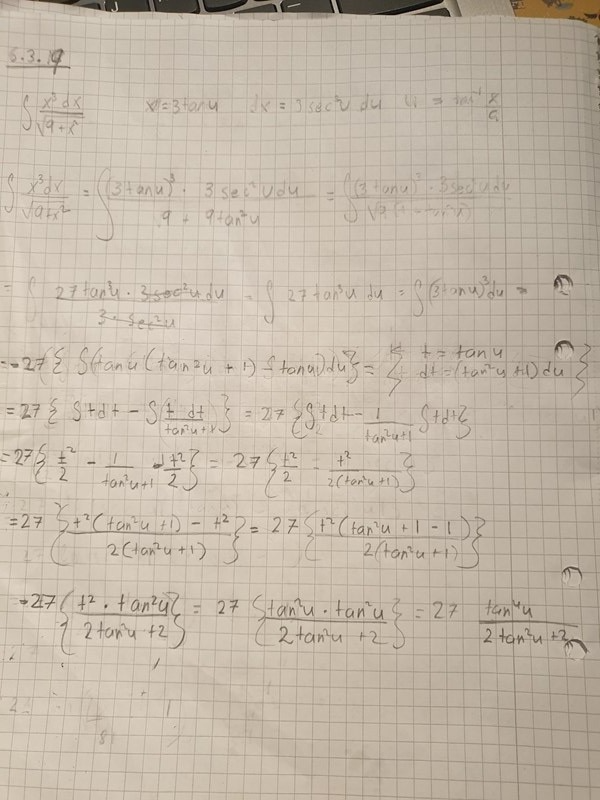
Du verkar göra t = tan(u) i båda integralerna. 

(I den andra integralen får du inte flytta ut faktorer med u utanför integralen, eftersom u är en funktion av t.)

Gör bara substitutionen t = tan(u) i den första integralen. Sedan återstår att substituera tillbaka till u och sedan till x. 

En faktor sec(u) verkar ha tillkommit i nämnaren. På slutet av ditt första papper bör det stå

$\displaystyle \int \tan^3u \sec u \ du$

Wolfram löser integralen utan tangens, med substitutionerna

u = x² 

s = u + 9

Med tangensspåret så får du byta ut tan²u mot sec²u - 1 och tänka på att d(sec u)/du = sec u tan u. 

Tack, löste den!