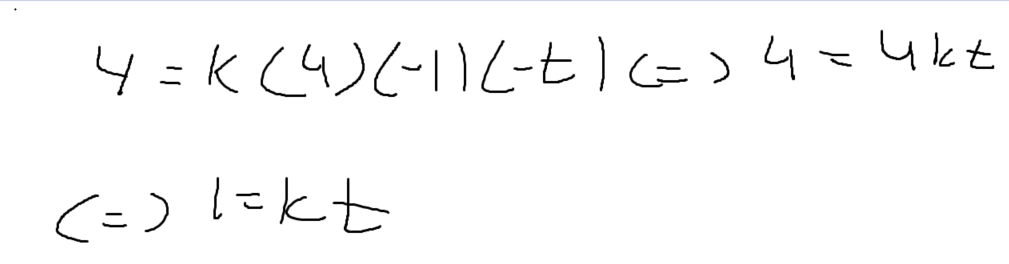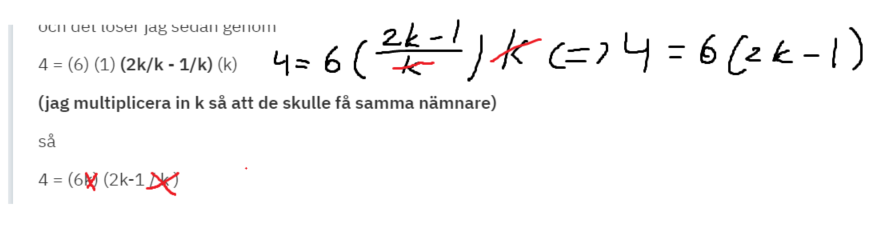ettan varifrån?

Jag skulle gissa på att personen hade räknat svaret och menade att skriva en 4:a men råkade skriva en 1:a eftersom man vet att 1=kt efter man räknat klart. 

Kan du bifoga tråden/svaret? 

För övrigt så ska du skriva 4a där så atT;

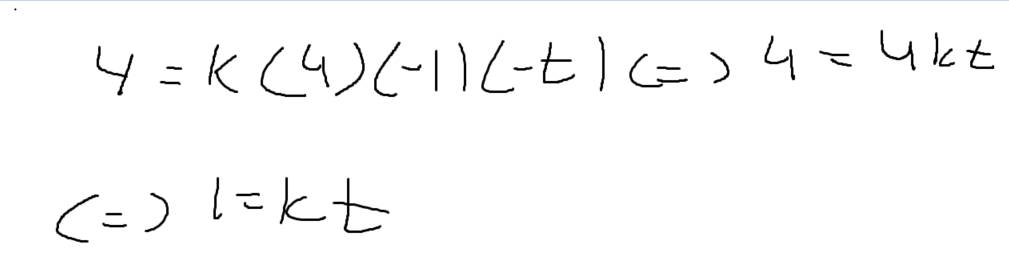
Dracaena skrev:

Jag skulle gissa på att personen hade räknat svaret och menade att skriva en 4:a men råkade skriva en 1:a eftersom man vet att 1=kt efter man räknat klart. 

Kan du bifoga tråden/svaret? 

För övrigt så ska du skriva 4a där så atT;

tack, här är tråden: https://www.pluggakuten.se/trad/uppgiftsbank-matematik-3-polynom-och-ekvationer/ 

och vad menar du med det här?

För övrigt så ska du skriva 4a där så atT; 

Vart står 4a?

Ah, tack!

Nej, det är bara slarv, det ska egentligen stå 4.

Faktorsatsen säger att ett polynom av grad $n$ kan skrivas på formen:

$k(x-x_n)(x-x_{n-1})....(x-x_1)(x-x_0)$

vi vet att graden är $n=3$ och givet är två nollställen:

$f(x)=k(x+4)(x-1)(x-x_0)$

Vidare vet vi att $f(0)=4$ samt att $f(2)=4$. Du kan använda $f(2)$ istället om du vill men $f(0)$ är ett väldigt bekvämt värde eftersom det blir mindre tal.

Hänger du med på varför det alltså ska vara 4 och inte 1?

Dracaena skrev:

Ah, tack!

Nej, det är bara slarv, det ska egentligen stå 4.

---

Faktorsatsen säger att ett polynom av grad $n$ kan skrivas på formen:

$k(x-x_n)(x-x_{n-1})....(x-x_1)(x-x_0)$

vi vet att graden är $n=3$ och givet är två nollställen:

$f(x)=k(x+4)(x-1)(x-x_0)$

Vidare vet vi att $f(0)=4$ samt att $f(2)=4$. Du kan använda $f(2)$ istället om du vill men $f(0)$ är ett väldigt bekvämt värde eftersom det blir mindre tal.

---

Hänger du med på varför det alltså ska vara 4 och inte 1?

ja, jag har kommit fram till

4 = (0+4) (0-1) (0-t) (k)

4 = k(4)(-1)(-t)

4 = 4kt

1 = kt

t = 1/k

så nu tar jag punkt (2,4) och sätter in i formeln...

4 = (2+4) (2-1) (2- (1/k) (k)

ser det rätt ut?

och det löser jag sedan genom

4 = (6) (1) (2k/k - 1/k) (k)

(jag multiplicera in k så att de skulle få samma nämnare)

så 

4 = (6k) (2k-1 / k ) 

som blir 

4 = ( 12k^2 - 6k )/ k

sedan dividerar jag med k och får

12k - 6 = 4

12k = 10 

k = 1,2 

, fast i detta fallet var ju t 1,2?

$f(2)=k(6)(-1)(2-t) = 12k - 6kt = 4 \iff 3k-\dfrac{3}{2}kt = 1$

Vi vet redan att $kt=1$ så om vi byter ut detta så får vi:

$3k-\dfrac{3}{2}\cdot 1 = 1 \iff k=...$

Dracaena skrev:

$f(2)=k(6)(-1)(2-t) = 12k - 6kt = 4 \iff 3k-\dfrac{3}{2}kt = 1$

Vi vet redan att $kt=1$ så om vi byter ut detta så får vi:

$3k-\dfrac{3}{2}\cdot 1 = 1 \iff k=...$

aa okej jag är med på er lösning. men bör inte min lösning också fungera? jag har egentligen substituerat tidigare och sen fått fram svar. ni hade substituerat lite längre ner mot svaret.

har jag räknat fel någonstans? eller varför fick inte jag samma svar?

Här blir det fel: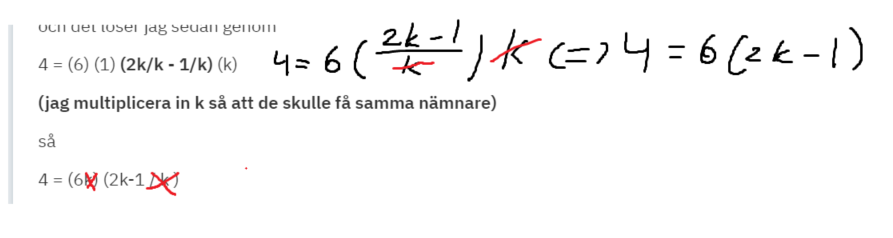

Dracaena skrev:

Här blir det fel:

jo men det är ju klart! tack snälla

Ingen fara. :)

Kommer du fram till rätt svar? 

Dracaena skrev:

Ingen fara. :)

Kommer du fram till rätt svar? 

japp! (: