Ersättningsresistans
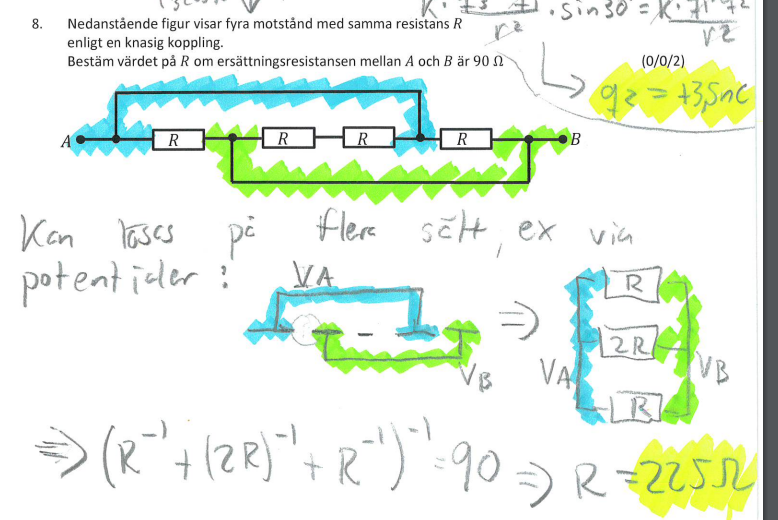
jag förstår inte alls den här uppgiften eller förklaringen. kan någon vänligen förklara?
Potentialerna VA och VB är färgmarkerade. Detta är gjort för att visa att den förenklade figuren är samma sak som uppgiftfiguren.
Du kan enkelt beräkna ersättningsresistansen i den förenklade figuren, eller hur?
Så din fråga kokar ner till hur man förenklar resistansnätet.
Titta på resistansen längst till vänster. Dess vänstra sida har potentialen VA, dess högra sida har potential VB. Det är exakt lika som den förenklade figuren.
Samma sak gäller för de övriga resistanserna då man jämför figurerna.
Hänger du med?
JohanF skrev:Potentialerna VA och VB är färgmarkerade. Detta är gjort för att visa att den förenklade figuren är samma sak som uppgiftfiguren.
Du kan enkelt beräkna ersättningsresistansen i den förenklade figuren, eller hur?
Så din fråga kokar ner till hur man förenklar resistansnätet.
Titta på resistansen längst till vänster. Dess vänstra sida har potentialen VA, dess högra sida har potential VB. Det är exakt lika som den förenklade figuren.
Samma sak gäller för de övriga resistanserna då man jämför figurerna.
Hänger du med?
aha men hur får de i den förenklade bilden resistansen 2R? Då måste man ju först passera den först R?!
Kan du formlerna för serie- och parallellkopplade motstånd?
Splash.e skrev:JohanF skrev:Potentialerna VA och VB är färgmarkerade. Detta är gjort för att visa att den förenklade figuren är samma sak som uppgiftfiguren.
Du kan enkelt beräkna ersättningsresistansen i den förenklade figuren, eller hur?
Så din fråga kokar ner till hur man förenklar resistansnätet.
Titta på resistansen längst till vänster. Dess vänstra sida har potentialen VA, dess högra sida har potential VB. Det är exakt lika som den förenklade figuren.
Samma sak gäller för de övriga resistanserna då man jämför figurerna.
Hänger du med?
aha men hur får de i den förenklade bilden resistansen 2R? Då måste man ju först passera den först R?!
Det är riktigt. Därför valde facit att förenkla dessa två resistanser tillsammans. Dvs vänstersidan av den vänstra resistorn har potentialen VA. Högersidan av den högra resistansen har potentialen VB.
Precis som i den förenklade figuren.
JohanF skrev:Splash.e skrev:JohanF skrev:Potentialerna VA och VB är färgmarkerade. Detta är gjort för att visa att den förenklade figuren är samma sak som uppgiftfiguren.
Du kan enkelt beräkna ersättningsresistansen i den förenklade figuren, eller hur?
Så din fråga kokar ner till hur man förenklar resistansnätet.
Titta på resistansen längst till vänster. Dess vänstra sida har potentialen VA, dess högra sida har potential VB. Det är exakt lika som den förenklade figuren.
Samma sak gäller för de övriga resistanserna då man jämför figurerna.
Hänger du med?
aha men hur får de i den förenklade bilden resistansen 2R? Då måste man ju först passera den först R?!
Det är riktigt. Därför valde facit att förenkla dessa två resistanser tillsammans. Dvs vänstersidan av den vänstra resistorn har potentialen VA. Högersidan av den högra resistansen har potentialen VB.
Precis som i den förenklade figuren.
Förlåt typo! Byt plats på VA och VB i ovanstående förklaring (men resultatet blir detsamma)
Jag förstår inte :(
Strömmen kan ju antingen gå genom den blå och sedan genom R - det är första parallelkopplingen
andra parallelkopplingen är genom första R mellan blå och grön och sedan följa den gröna nedre grenen
den sista parallelkopplingen är genom den första R mellan blå och grön, sedan genom 3 st till R i serie. Då blir ersättningsresistanse 4R. Så varför står det 2R i förenklingen?
Jag förstår att det kan vara lite svårt att greppa att man kan titta på en resistorlönk i taget sådär, utan att behöva ta hänsyn till vad som händer "runtomkring".
Jag kan förklara lite mer, senare i em, varför man kan det. Men det är av samma anledning som du kan förenkla med serie- och parallellkopplingar (som du upptäckte att du inte kunde i denna uppgift, eftersom resistorerna är kopplade så "knasigt"
JohanF skrev:Jag förstår att det kan vara lite svårt att greppa att man kan titta på en resistorlönk i taget sådär, utan att behöva ta hänsyn till vad som händer "runtomkring".
Jag kan förklara lite mer, senare i em, varför man kan det. Men det är av samma anledning som du kan förenkla med serie- och parallellkopplingar (som du upptäckte att du inte kunde i denna uppgift, eftersom resistorerna är kopplade så "knasigt"
Om du tänker på det, det enda som avgör vilken ström som flyter genom en resistor, är potentialskillnaden mellan de båda sidorna på resistorn, och resistorns värde (). Det spelar alltså ingen som helst roll om strömmen flyter på något kringelikrokigt sätt före eller efter den resistor som du beräknar strömmen genom, bara du vet spänningen över den.
Så länge du ser till att spänningen mellan två noder och strömmen mellan dessa noder förblir desamma, så kan du ersätta den resistans som finns däremellan med precis vad du vill.
Det är till exempel av detta skäl man kan titta på olika delar av ett resistansnät, och beräkna ersättningsresistanser där det finns parallell- och seriekopplade resistanser, utan att ta hänsyn vad som finns "runt omkring". Sådana uppgifter har du säkert räknat flera av förut.
Hänger du med nu på varför man kan göra som facit har gjort?
Splash skrev "Strömmen kan ju antingen gå genom den blå och sedan ..."
Tror du missuppfattar hur strömmen "beter sig".
Strömmen går genom samtliga motstånd i detta exempel. Den kan inte välja att hoppa över något motstånd här.


