Envariabelanalys - Varför är följande resonemang fel?
Jag ska bestämma ifall följande integral konvergerar/divergerar:
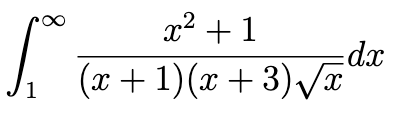
Mitt resonemang lyder som följande:
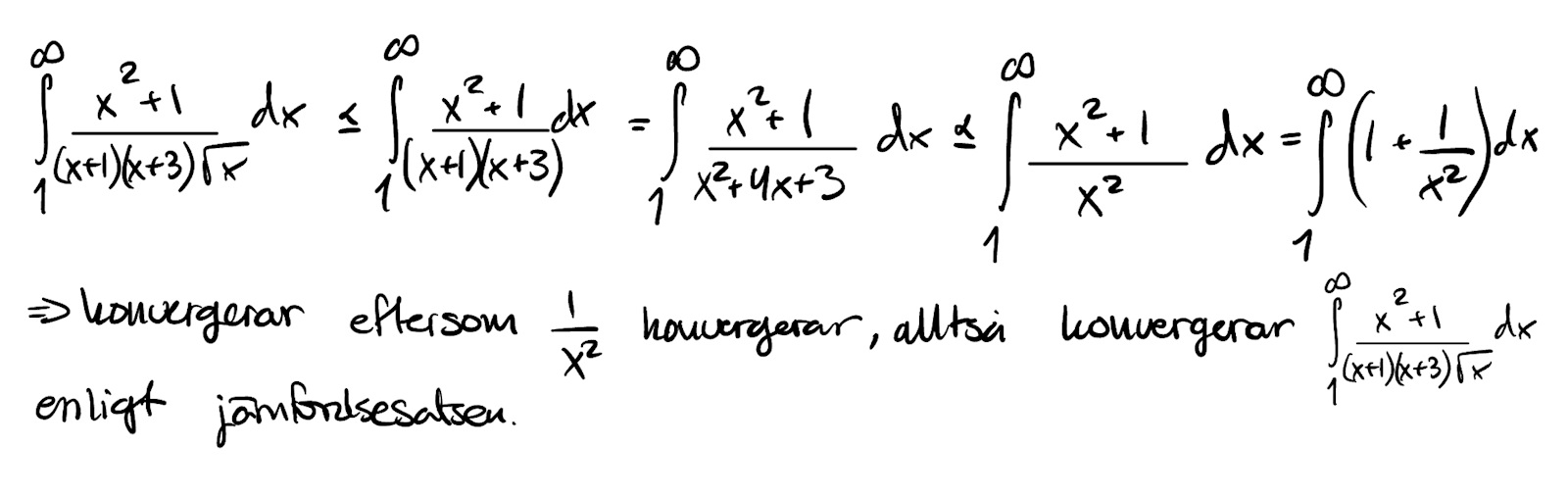
Detta är fel, eftersom facit säger att den divergerar. Varför är det fel?
Du fuskar lite, du har ju , visserligen är konvergent med de gränserna men är inte konvergent.
När x går mot oändligheten går 1/x mot 0, så för större och större x går allting mot y=1, och arean är då oändlig.
Dracaena skrev:Du fuskar lite, du har ju , visserligen är konvergent med de gränserna men är inte konvergent.
När x går mot oändligheten går 1/x mot 0, så för större och större x går allting mot y=1, och arean är då oändlig.
Hänger inte riktigt med. är konvergent då borde väl också vara det eftersom 1 endast är konstant?
Eller tror jag förstår nu. Stämmer följande?
och eftersom divergerar gör även ursprungsintegralen det. För att ursprungsintergralen ska konvergera måste båda delintegralerna göra det.
Precis! Det jag menade i #2 är följande (samma som du skrev algebraiskt):
https://www.desmos.com/calculator/8j4tn4ofhi
Integralen av f(x) är area under kurvan, om f(x) går mot y=1 så kommer integralen aldrig vara konvergent eftersom du kommer att ha oändligt med area att addera upp. Precis det som du uttryckte snyggt algebraiskt i #4
Dracaena skrev:Precis! Det jag menade i #2 är följande (samma som du skrev algebraiskt):
https://www.desmos.com/calculator/8j4tn4ofhiIntegralen av f(x) är area under kurvan, om f(x) går mot y=1 så kommer integralen aldrig vara konvergent eftersom du kommer att ha oändligt med area att addera upp. Precis det som du uttryckte snyggt algebraiskt i #4
Tack för hjälpen!


