Envariabelanalys - bevisa addititivet för gränsvärden
God eftermiddag!
I vår kurs i envariabelanalys har vi en bevislista med olika bevis vi ska kunna inför sluttentan. Jag håller nu på att gå igenom denna och försöka komma fram till bevisen själv i första hand. Just nu jobbar jag med följande bevis:
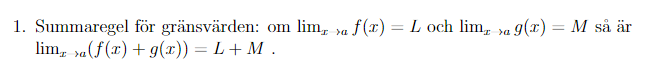
Jag har en lösning och jag undrar om den är korrekt. Den ser ut så här:
Givna är:
Det vi då ska visa är att:
Vi börjar med att införa en ny variabel enligt . Vi kan då skriva om (1) och (2) enligt:
Detta borde medföra att:
Med hjälp av triangelolikheten kan vi sedan dra slutsatsen att:
Eftersom kan väljas godtyckligt, kan även väljas godtyckligt. Således har vi att:
Rackarns, min telefon dog precis innan jag skulle posta mitt svar...
När du säger "borde medföra att", så är det lite oklart. Du vet inte a priori att du kan hitta ett sådant delta för f(x)+g(x), utan det du ska bevisa är att givet något fixt epsilon, så finns det ett delta sådant att...
Notera att för ett givet epsilon, så kan du hitta delta_1 sådant att |x-x0|<delta_1 medför |f(x)-L|<epsilon, men detta delta_1 är inte nödvändigtvis samma för g(x) och samma epsilon.
Visa spoiler
Använd definitionen på f och g där du hittar delta_1 och delta_2 för värdet epsilon/2. Definiera sedan ett delta utifrån dessa.
Borde jag inte bara kunna välja det som är mindre av de två? Om jag vet att samt att , så borde det väl också gälla att ?
Testa!
När jag testar numeriskt verkar det stämma. Låt säga att vi undersöker gränsvärdet i punkten för funktionen och att vi väljer . Då måste vi hitta ett sådant att . Om vi väljer t.ex. funkar det. Och vi kan ju alltid välja ett mindre och mindre , och fortfarande ha att det medför . Så om man hittar ett för ett givet , kan man alltid göra sitt mindre.
Stämmer den slutsatsen?
Rent grafiskt vill vi ju ligga på kurvan mellan dessa horisontella gränser:
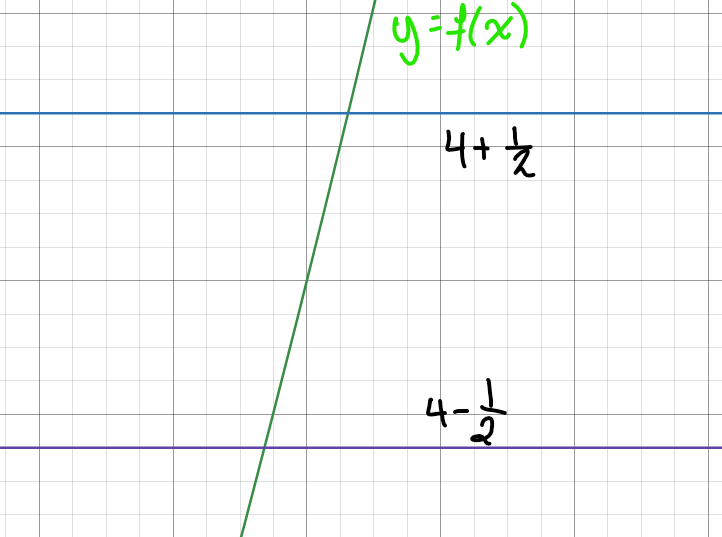
Och det kan man ju göra med oändligt många under en viss gräns.
Ja, eftersom |x-x0| < d ==> |x-x0| < d' för alla d' >= d. Men det jag tänkte på var att givet ett epsilon kan du hitta d1 och d2 sådana att |f-L|<epsilon/2 för det första, och |g-M|<epsilon/2 för det andra. Och så kan du ju ta d = min{d1, d2} och dra slutsatsen att när |x-x0|<d, så är |f(x) - L| + |g(x) - M| < epsilon/2 + epsilon/2. Det var så jag tänkte.
Kan tyvärr inte skriva riktiga ekvationer från telefonen, hoppas det är läsbart ändå.
Och så kan du ju ta d = min{d1, d2}
Jo precis, om jag förstår notationen rätt var det precis dit jag ville komma. Det vi säger här är väl i princip att vi väljer ut det minsta av och och sätter det som vårt nya ?
Japp, för det mindre av de två så gäller båda olikheterna så då kan du köra triangelolikheten och avsluta beviset.
Okej, så ett nytt försök:
Låt och låt . Vi har således att:
Låt
Detta ger sammantaget :
Detta innebär med andra ord att:
Eftersom kan väljas godtyckligt kan även väljas godtyckligt. Således har vi utifrån och att:
Ser det bra ut nu? :D
Ja, fast du behöver inte blanda in en ny variabel . Enligt definitionen av gränsvärde kan du hitta ett delta för varje positivt reellt tal. Så i detta fall använder vi definitionen på f och g var och en, där vi väljer vi talet och får då två olika delta. Det är helt korrekt det du skrivit, det är bara att du slipper argumentet att "eftersom kan väljas godtyckligt, kan även väljas godtyckligt" om du gör så.
Hur ska man egentligen hantera x=a? Hur blir det när man gör som du nu, dvs typ ignorerar det?
Annars borde man väl sätta 0<abs(x-a)<delta alternativt ta ut a från (D\{a})?
Vår föreläsare tar ut a från D och i kursboken (Analys i en variabel. Persson och Böiers.) pratar de om lite olika varianter men förstår inte riktigt skillnaden. Har ni några tankar?
alternativt ta ut a från (D\{a})?
Japp, i mitt huvud hade jag redan gjort det men tydligen inte på pappret.
Det som gör det lite förvirrande ibland är att --kriteriet för kontinuitet är identiskt men utan kravet att . Så ibland skriver man på rent muskelminne och då blir det så här!
Ja, det är egentligen rimligare att utesluta x=a ur definitionen som du skriver. Annars antar man att funktionen är kontinuerlig i x=a, vilket inte behöver vara fallet. Till exempel behöver f inte vara definierad i x=a även om gränsvärdet existerar.
Okaj. Och att ta ut från D eller sätta avståndet till a strikt större än 0 är samma sak?




