Enhetscirkeln

hej! Håller på med ett antal uppgifter där man ska beräkna vinklar i sinus och cosinus UTAN miniräknare, och jag undrar om någon kan förklara hur man ska gå tillväga med hjälp av enhetscirkeln och att rita ut trianglar. Jag förstår själva principen men inte hur man ska gå tillväga för att få fram att till exempel sinus(120 grader)= sqrt 3/2

tacksam för hjälp med formel eller liknande hur man ska tänka för vinklar man inte bara kan memorera

Kika på enhetscirkeln, finns det någon annan vinkel som har samma värde som sin(120 grader)?

pepparkvarn skrev:
Kika på enhetscirkeln, finns det någon annan vinkel som har samma värde som sin(120 grader)?

Ja, sin(60 grader) men hur ska man beräkna detta när man varken kan använda miniräknare eller tabell? Är det bara att memorera alla vanliga vinklars värden?

Det finns några få vinklar vars sinus-och cosinusvärden du behöver memorera. Egentligen behöver du bara komma ihåg två trianglar - "en halv kvadrat" (med vinklarna 45^o, 45^o och 90^o och sidorna 1, 1 och $\sqrt2$ ) och "en halv liksidig triangel" (med vinklarna 30^o, 60^o och 90^o och sidorna 1, 2, $\sqrt3$ ). Du kan använda Pythagoras sats om du inte kommer ihåg siffrorna. Kombinera detta med enhetscirkeln och du har sinus och cosinus för 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 330 och 360 grader, bara fö ratt ta det första varvet. Allt detta är mycket lättare att komma ihåg som bilder än som text!

För att svara på din specifika fråga, så

rita en enhetscirkel
rita in vinkeln 120^o (snett upp åt vänster, brantare än 45^o eftersom det skulle motsvara 135^o)
Du behöver komma ihåg att sinus-värdet är det man läser av på y-axeln (jag brukar tänka på att cosinus och sinus skall vara i alfabetisk ordning, precis som x och y) så därför skall du rita en vågrät linje från den punkt där vinkelbenet skär cirkeln och åt höger, tills den skär cirkeln på andra sidan
Dra en linje från denna nya punkt ner till x-axeln. Du har gjort en rätvinklig triangel. Du bör kunna komma fram till att denna triangel har vinkeln 60^o vid origo. Sinus för 60^o är motstående katet/hypotenusa i "en halv liksidig triangel", alltså $\frac{\sqrt3}{2}$ . Detta är samma värde so sinus för 120^o, det syns på bilden.

Behöver du mer hjälp, så berätta vad det är du fortfarande undrar över och fråga igen!

Nej du behöver inte lära dig detta utantill.

Med hjälp av tankestöden "halv kvadrat" och "halv liksidig triangel" så är det lätt att härleda sinus, cosinus och tangensvärdena för vinklarna 30°, 45° och 60°. Med hjälp av enhetscirkeln så är det sedan lätt att hitta motsvarande värden i övriga kvadranter.

Halv kvadrat:

Rita en kvadrat med sidlängd 1.

Dela kvadraten i två halvor med hjälp av en diagonal.

Halvorna har då formen av rätvinkliga trianglar med vinklarna 45°, 45° och 90°.

Pythagoras sats ger att hypotenusans längd är $\sqrt{2}$ .

Eftersom sin(v) = "motstående katet"/"hypotenusa" och cos(v) = "närliggande katet"/"hypotenusa" så kan du nu enkelt beräkna sin(45°) och cos(45°).

Halv liksidig triangel:

Rita en liksidig triangel med sidlängd 1, vinklarna är alla 60°.

Dela triangeln i två lika stora delar med hjälp av en bisektris.

Varje triangelhalva är då en rätvinklig triangel med vinklarna 30°, 60° och 90°.

Kan du fortsätta själv?

Jag bidrar med några, inte särskilt vackra, illustrationer:

En kvadrat där alla sidor har längden ett:

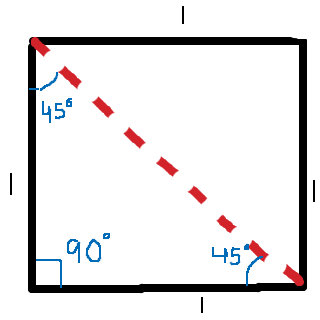
Härifrån kan du utläsa värdena $\sin (45 °)$ och $\sin (90 °)$ (samt respektive värden för cosinus och tangensvärdet av 45 grader).

En liksidig triangel där alla sidor har längden ett:

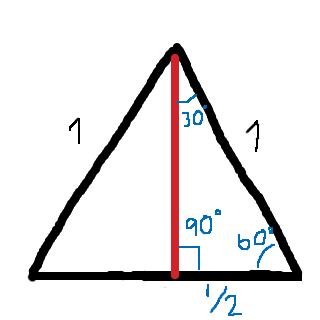
Härifrån kan du utläsa $\sin (30 °), \sin (60 °)$ och $\sin (90 °)$ (samt respektive värden för cosinus och tangens för 30 och 60 grader).

Edit: Se Yngves kommentar nedan. :)

pepparkvarn skrev:
Jag bidrar med några, inte särskilt vackra, illustrationer:
...

En figur behöver inte alls vara fint ritad. Dina figurer funkar utmärkt!

-----

Det enda jag har att anmärka på är att det inte går att utläsa vare sig sin(90°), cos(90°) eller tan(90°) ur någon av figurerna.

De trigonometriska funktionernas värden för vinklarna 0° och 90° bör man lära sig utantill alternativt hitta med hjälp av enhetscirkeln.

Yngve skrev:
pepparkvarn skrev:
Jag bidrar med några, inte särskilt vackra, illustrationer:
...
En figur behöver inte alls vara fint ritad. Dina figurer funkar utmärkt!
-----
Det enda jag har att anmärka på är att det inte går att utläsa vare sig sin(90°), cos(90°) eller tan(90°) ur någon av figurerna.
De trigonometriska funktionernas värden för vinklarna 0° och 90° bör man lära sig utantill alternativt hitta med hjälp av enhetscirkeln.

Tack tack! 🥰

Tekniskt sett går det att utläsa sin(90). Om vi utnyttjar att sinus är motstående sida dividerat med hypotenusan, får vi att sin(90) = 1. Det är fult, men det går. Däremot går det inte med cos(90) - det ska jag ändra - , eller med tan(90) - det har jag aldrig påstått. :)

pepparkvarn skrev:

Tack tack! 🥰

Tekniskt sett går det att utläsa sin(90). Om vi utnyttjar att sinus är motstående sida dividerat med hypotenusan, får vi att sin(90) = 1. Det är fult, men det går. Däremot går det inte med cos(90) - det ska jag ändra - , eller med tan(90) - det har jag aldrig påstått. :)

Jaha OK det stämmer ju att motstående sida till vinkeln 90° är hypotenusan. Och det stämmer ju att kvoten mellan hypotenusans längd och hypotenusans längd är lika med 1.

Men såvitt jag minns av "rätvinklig triangel-definitionen" av sinus (och cosinus) så gäller den endast för de spetsiga vinklarna i en rätvinklig triangel. Kanske någon som har bättre koll kan fylla i här.

Du har rätt i att du inte påstått att tan(90°) går att utläsa. My bad.

Yngve skrev:
pepparkvarn skrev:
Tack tack! 🥰

Tekniskt sett går det att utläsa sin(90). Om vi utnyttjar att sinus är motstående sida dividerat med hypotenusan, får vi att sin(90) = 1. Det är fult, men det går. Däremot går det inte med cos(90) - det ska jag ändra - , eller med tan(90) - det har jag aldrig påstått. :)
Jaha OK det stämmer ju att motstående sida till vinkeln 90° är hypotenusan. Och det stämmer ju att kvoten mellan hypotenusans längd och hypotenusans längd är lika med 1.
Men såvitt jag minns av "rätvinklig triangel-definitionen" av sinus (och cosinus) så gäller den endast för de spetsiga vinklarna i en rätvinklig triangel. Kanske någon som har bättre koll kan fylla i här.

Det låter bekant att sådant är fallet, jag menar bara att det går. :)

Dock blir det ju lite skumt för cosinus. Du har helt rätt i att enhetscirkeln är mycket bättre i dessa fall. :)

Svara

Visa senaste svar