Enhetscirkel-ta reda på kordinater


Försöker lösa med hjälp av enhetscirkeln men fastnar för att det finns för många variabler. Men ser att man kan lösa den genom att få 2 trianglar med lika lång hypotenusa då båda är cirkelns radie och då måste de ha samma katetrar. Dock så handlar avsnittet om enhetscirklar så undrar hur man löser den så eller gör jag rätt? Tack på förhand.
Zart skrev:
Försöker lösa med hjälp av enhetscirkeln men fastnar för att det finns för många variabler. Men ser att man kan lösa den genom att få 2 trianglar med lika lång hypotenusa då båda är cirkelns radie och då måste de ha samma katetrar. Dock så handlar avsnittet om enhetscirklar så undrar hur man löser den så eller gör jag rätt? Tack på förhand.
Du verkar tänka rätt. Alla rätvinkliga trianglar (med ett icke-rätt hörn i origo) som du ritat in i enhetscirkeln har radien 1. I ditt fall blir vinkeln mellan y-axeln och linjen från origo till Q lika med v.
Tack för svaret men förstår inte vad du menar med vinkeln mellan y-axeln och linjen från origo är v. För när man pratar om enhetscirklar så går vinkeln från positiva x-axeln till den negativa. Menar du att den då går från den negativa till Q? Såg någon göra likadant med trianglar men undrar fortfarande om man kan lösa uppgiften med enhetscirkelns definition alltså med sin v och cos v
Ser du att de båda trianglarna är likformiga?
ja
Ser du också varför koordinaterna blir som de blir? Man kan använda sig av definitionerna för trigonometriska funktioner i en rätvinklig triangel för att härleda detta.
Skulle du kunna visa det?
Är du med på att för alla punkter på enhetscirkeln gäller det att de har koordinaterna (cos(v), sin(v))?
ja
Börja med att titta på den högra triangeln i första kvadranten .Hur lång är den motstående kateten i denna triangel? (Hypotenusan är 1, cirkelns radie.)

Kommer hit sen tar det stopp vet inte om jag ska skriva v=sin^-1(a) och V=cos^-1(b) sen bara lösa det men tror inte att det funkar och vet inte hur jag skulle göra i så fall
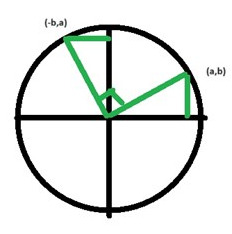
Är du med på att vinkeln mellan y-axeln och linjen från origo till Q är lika med v? Är du med på att de båda sidor jag har markerat är b respektive a?

ja
Är du med på att i den högra triangeln har motstående katet längden a och närliggande katet b?
Är du med på att i den vänstra triangeln har motstående katet längden a och närliggande katet b?
Ja till det första och nej till det andra. Vet inte hur man kommer fram till det. Om man ska räkna att de har lika långa hypotenusor och därav har lika stora katetrar
Punkten P har koordinaterna (a,b) = (cos(v), sin(v)). Vilka koordinater har punkten Q? Tänk dels på hur långa de båda kateterna i triangeln är, dels på att punkten skall hamna i rätt kvadrant.
(-b,a) men kan man inte komma fram till det med en uträkning
Man kan lära sig en massa regler utantill, men det är mycket bättre att läara sig resonera så som vi har gjort här. Det är så lätt att minnas en regel NÄSTAN rätt och råka göra fel med t ex minustecken, så därför rekommenderar jag resonemang istället.
Ja men man måste också visa resonemang med hjälp av uträkningar som stödjer vad man påstår
man kan även lösa den för linjerna p till origo och Q till origo är vinkelräta mot varann så b/a *x=-1 så då är Q=a/(-b). Men undrar fortfarande om man kan ta fram svaret med sin v och cos v
Man motiverar genom att säga att de båda trianglarna är likformiga och fortsätta därifrån.



