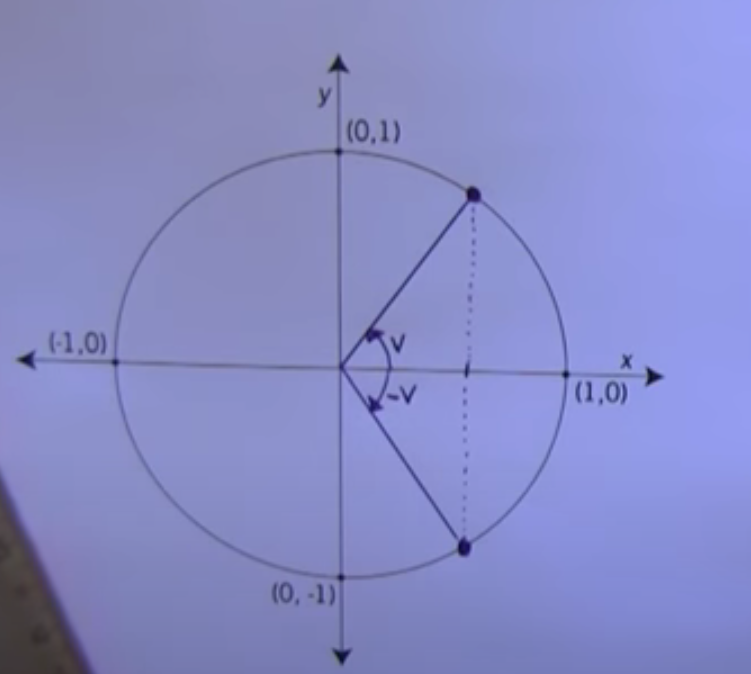
Enhetcirkeln.

ii_noor06 skrev:

Hej, jag undrar på en jätteviktig sak.

När jag kollade runt på videos om enhetscirkeln så såg jag mycket spegling. Varför speglar de t.ex triangeln han har ritat upp på cirkeln? Vad är poängen när han speglar den, det är så han säger "nu speglar vi den på samma sätt" Försåt faktiskt inte.

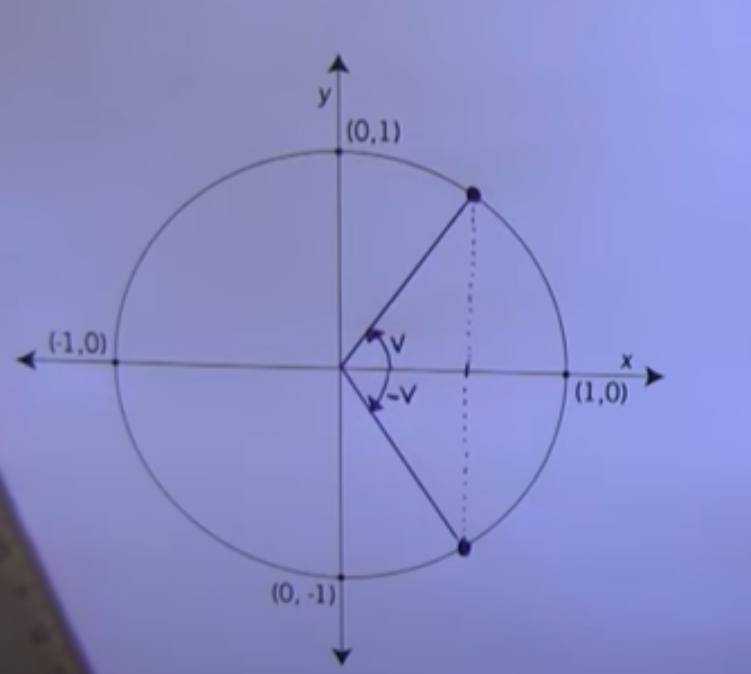
Det ör meningen att du skall se att cos(-v) = cos(v), men att sin(-v) = -sin(v).

Ahaa. Vi säger cirkeln här okej.

Vart finns cos, sin och tan? Och varför kallas de så? Varför kallade ni de så? är det inte lättare och säga typ hypotenusan nånting eller  vi vet vad sidorna kallar med hjälp av formeln a²+b²= c² kan man inte säga a sidan någonting?

Vart finns cos, sin och tan?

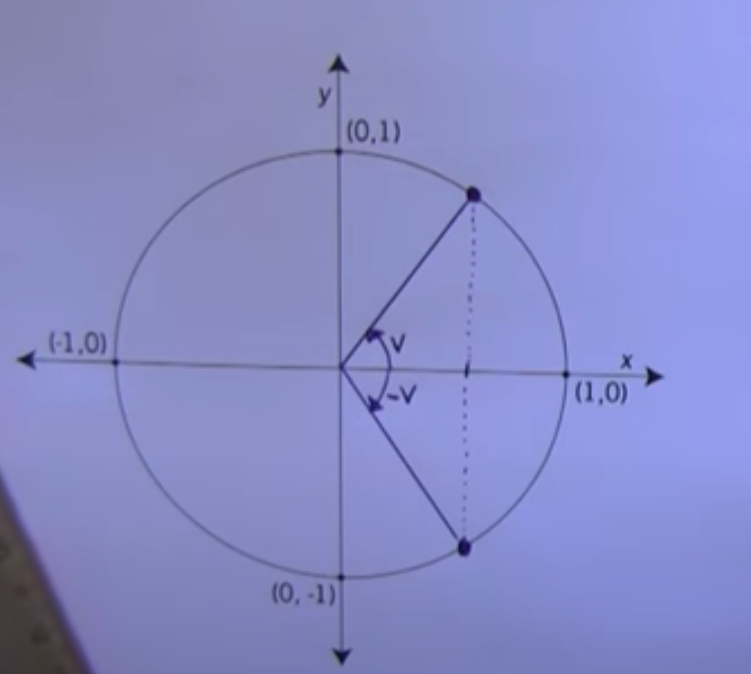
Cirkeln är en enhetscirkel, d v s en cirkel med centrum i origo och radien 1. Om man fitar en vinkel (uppåt från positiva x-axeln) som har storleken v, så är sin(v) = y-värdet för den punkt där vinkelbenet skär cirkeln, cos(v) = x-värdet för den punkt där vinkelbenet skär cirkeln och tan(v) = sin(v)/cos(v), eller riktningskoefficienten för vinkelbenet.

Och varför kallas de så?

Här är en förklaring.

Varför kallade ni de så?

Det är väldigt användbart, och heter ungefär likadant på många språk

är det inte lättare och säga typ hypotenusan nånting eller vi vet vad sidorna kallar med hjälp av formeln a²+b²= c² kan man inte säga a sidan någonting?

Nej, men du har helt rätt i att det i princip är Pythagoras sats i förklädnad. Det är i många sammanhang praktiskt att kunna gå från vinkeln till sidan - man skulle kunna säga att man har räknat ut det förhållandet för varje storlek på vinkel en gång för allan.

Tack för förklaringen!