Energiprincipen (hylsa, trissa och vikt)
Har fastnat på en uppgift i mekanik. Dels så undrar jag om man får sätta olika nollpunkter för hylsan resp. vikten? Känns som de mest rimliga med tanke på att man inte vet skillnaden i höjd mellan hylsan och vikten i läge 1.
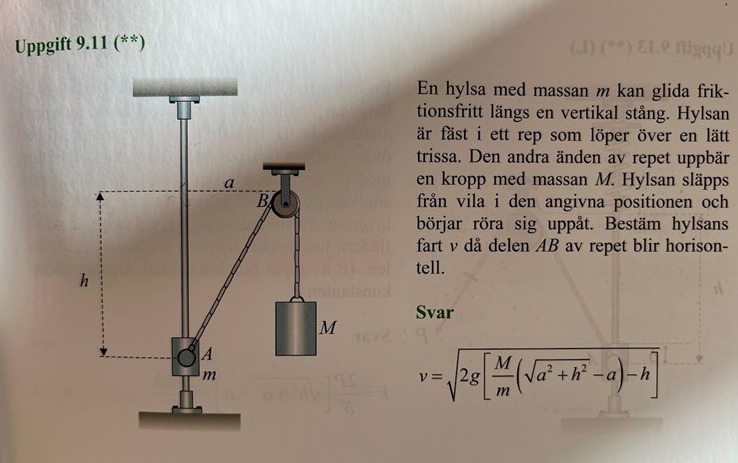
Iallafall, först tänkte jag:
Läge 1:
Hylsan: potentiell energi = 0, kinetisk energi = 0
Vikten: potentiell energi = MgH, kinetisk energi = 0
Läge 2:
Hylsan: potentiell energi = mgh, kinetisk energi = mv^2/2
Vikten: potentiell energi = 0, kinetisk energi = 0
Men sen kom jag på att om vi sätter nollnivån för vikten vid viktens position i läge 2 så borde den väl ha kinetisk energi (Mv^2/2) i läge 2? Men jag lyckas inte få till det så det matchar svaret....

TM beror väl inte på var du sätter nollnivån för den potentiella energin. Hur tänkte du då?
Ja, sorry - tänkte fel, som att den "stannar" vid nollnivån. Hur som helst!
Eftersom vi har kinetisk energi även för vikten i läge 2 så blir ekvationen:
Så då stämmer det inte överens med facit. Vad gör jag för fel?
Vilken hastighet har vikten vid läge 2? Du antar att vikten har samma hastighet (fart) som hylsan i detta läge. Är detta verkligen korrekt?
Tack! Okej, då inför jag v1 och v2 för m och M:
Suck... Får verkligen inte till det här
Du kan inte använda formeln för fritt fall på massan M, den sitter ju fast i ett rep.
v1 och v2 är inte oberoende och beror dessutom på hylsans läge.
Härled samband mellan v1 och v2 som beror på hylsans läge. (Spoiler: v2 = 0 i läge 2).
Nu förstår jag ingenting. Om v2 = 0 i läge 2 så har den ju ingen kinetisk energi? Samt om hylsan har hastighet måste ju vikten också ha det?
Nja, så är det faktiskt inte. Räkna på det så får du se.
Förstår inte riktigt... Samband mellan v1 och v2 beroende på hylsans läge? Menar du potentiell och kinetisk energi för respektive föremål eller?
Nej, det är ett rent kinematiskt samband.
Jahapp, kopplar inte vad du syftar på för samband
Svarar mer utförligt senare.
Din ekvation är nästan rätt, men tänk på att och
Lös ut
Det är ju detta jag inte förstår. Om vikten HAR kinetisk energi vid nollnivån så kan väl inte v2 vara 0?
? Så då har den ingen kinetisk energi vid läge 2?
Den stora vikten har ingen kinetisk energi eftersom dess hastighet är noll i läge två.
Däremot har vikten såklart ÄNDRAT sin potentiella energi (lägesenergi). Den har ju flyttat sig nedåt.
Det din ekvation säger är att ändringen i den stora viktens potentiella energi, , ska motsvara ändringen i den lilla viktens totala mekaniska energi
Jag tycker att du ska ställa upp en ekvation för repets längd och sedan derivera den för att få fram ett samband mellan hastigheterna om du inte genast inser varför
Sedan kan du göra en energijämförelse mellan läge 1 och läge 2, notera att
Se bild nedan.
Vi kallar hylsans läge relativt ursprungsläget x. Avståndet från hylsan till trissan är L.
Då gäller det att v1 = och att v2 = . Eller hur?
Enligt Pytagoras så har vi att
L2 = (h-x)2 + a2. Vi deriverar båda sidor av denna likhet map t (tiden).
.
Detta ger oss
v2 = v1.
I läge 2 befinner sig hylsan i nivå med trissan, så x = h, och v2 blir noll oavsett vad v1 har för värde.


