energiprincipen
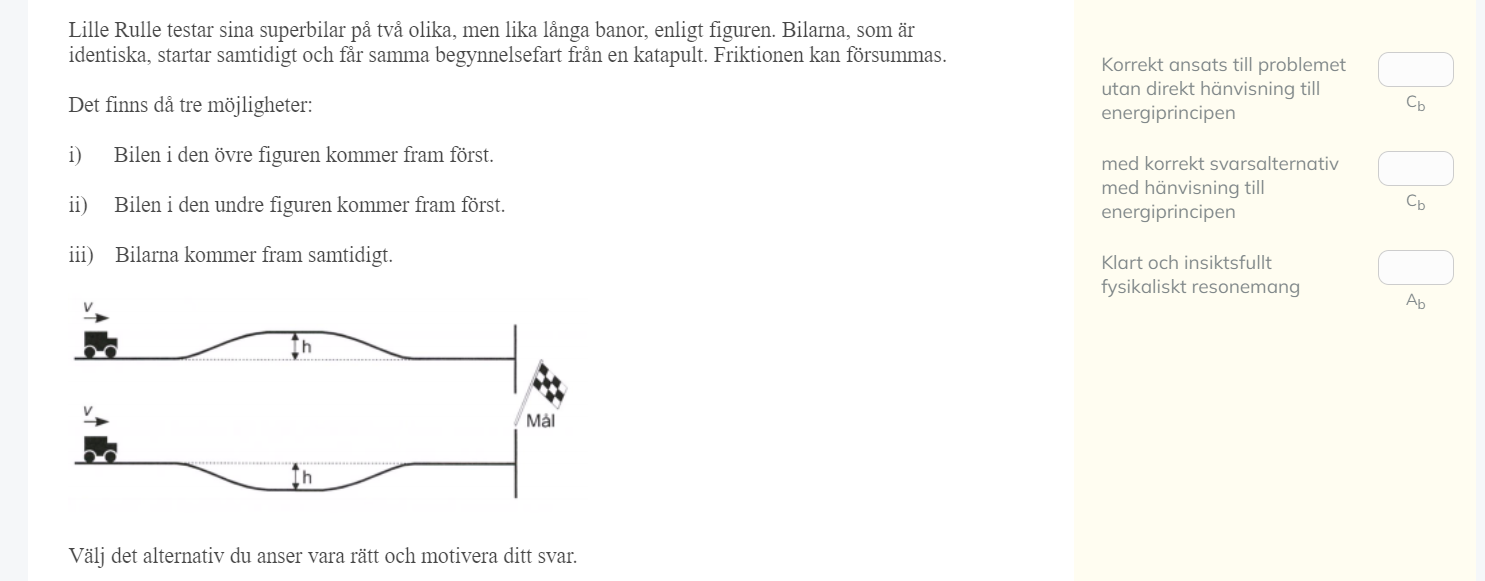
Kan någon förklara varför den nedre bilen kommer först?
Det sker en energiomvandling. Jag trodde först att båda kom fram samtidigt men det var fel. Den övre bilden har bilen rörelseenergi utan lägesenergi. Sedan får den lägesenergi vid kullen och rörelseenergi också. Sedan omvandlas lägesenergin till rörelse nerför backen.
I den andra bilen är gropen nollnivån. Innan gropen är det då lägesenergi och rörelse energi. I gropen är det bara rörelseenergi och efter gropen är det både rörelse och lägesenergi. Stämmer det? eller har jag fel?
Bilen har en viss Ek som minskar efter stigningen men ökar efter nedförsbacken.
I översta fallet kan vi tänka att bilen har 10 i energi. Efter backen får den 5 energi, och åker därmed med hastigheten som nås då energin är 5. I nedförsbacken blir den 10 igen och resten av vägen åker den med v.
I nedersta fallet har bilen återigen 10 energi, därefter ökar den till 15 energi genom gropen för att sedan efter uppförsbacken ur gropen tappa 5 energi och återgå till v.
Kan du utifrån detta resonemang förstå varför den nedre är snabbare? (talen har ingen specifik betydelse mer än en representation)
Tänk dig nollnivån för potentiell energi på den nivå som bilarna startar istället. Bilarna har samma kinetiska energi (därmed samma hastighet) när de åker på den nivån. Skillnaden mellan bilarnas hastigheter är alltså under den buktiga delen av banan. Vem har högst hastighet där?
Den bil vinner som har högst medelhastighet.
asså den första bilen behöver gå långsammare och därmed "spara energi" för den potentiella energin som sedan omvandlas till rörelseenergi nerför backen. Men i den andra så får bilen mer rörelseenergi som sedan omvandlas till potentiell energi. Jag förstår inte riktigt hur man tänker. Går det snabbare i den andra eftersom den inte behöver potentiell energi.
Vilken väg skulle du vilja ta om du cyklade?
den andra för man behöver inte anstränga sig lika mycket.
Såhär tänker jag:
Gemensamt för båda bilarna:
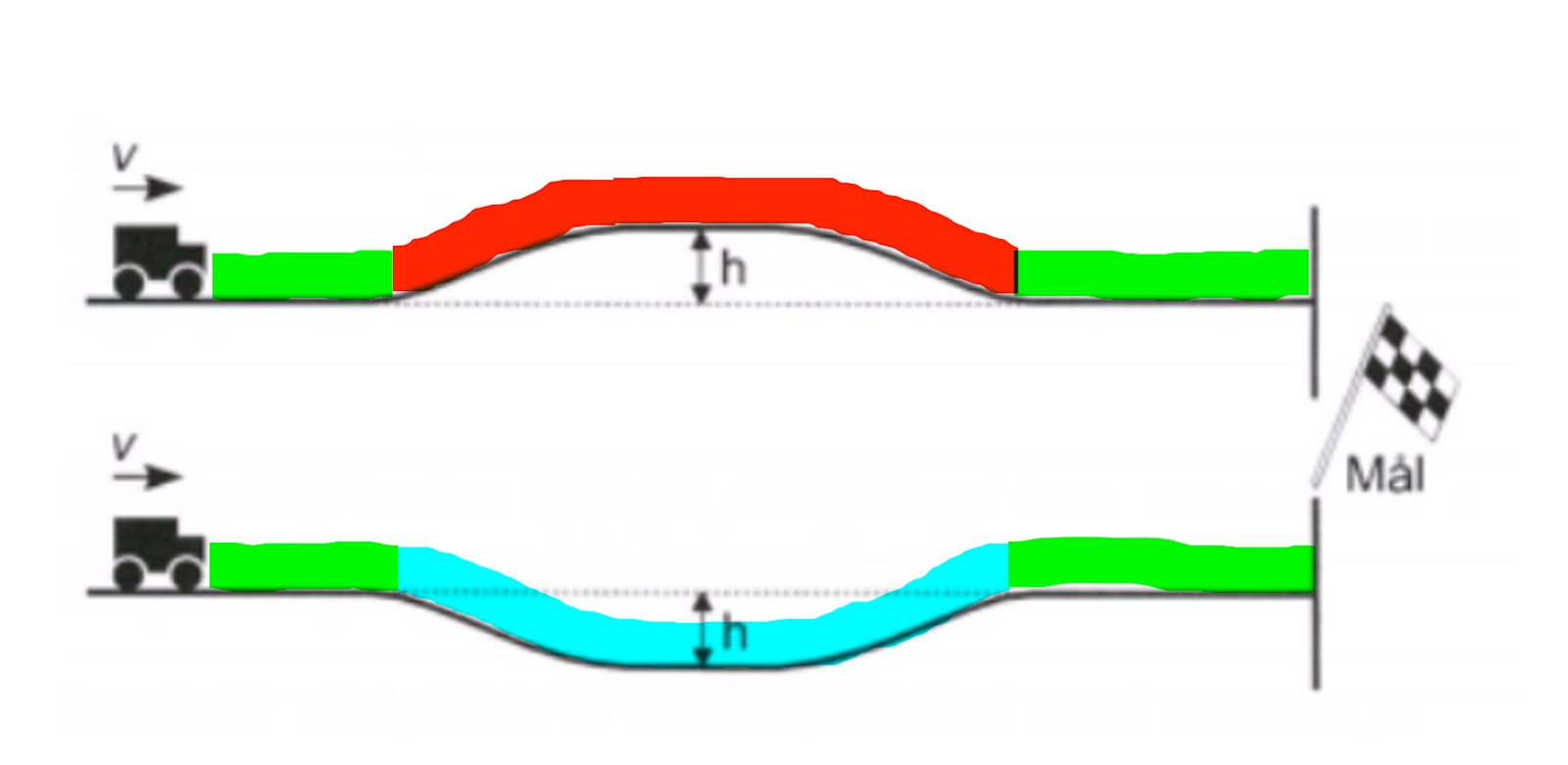
De grönmarkerade sträckorna är den kinetiska energin lika stor som bilarna fick av katapulterna, dvs under de grönmarkerade sträckorna kör bilarna med samma hastighet som utgångshastigheten.
Undre bilen:
När bilen kör den blåmarkerade sträckan så är bilens potentiella energi mindre än när den fick sin utgångshastighet. Det innebär att bilens kinetiska energi ör högre, dvs bilens hastighet är större än utgångshastigheten.
Övre bilen:
När bilen kör den rödmarkerade sträckan så är bilens potentiella energi högre än när den fick sin utgångshastighet. Det innebär att bilens kinetiska energi är mindre, dvs bilens hastighet är lägre än utgångshastigheten.
Detta innebär att den undre bilen kommer att köra sin blåmarkerade sträcka med högre hastighet än den övre bilen kör sin rödmarkerade sträcka. Eftersom dessa sträckor är lika långa. så kommer den undre bilen att köra den blåmarkerade sträckan under kortare tid än den övre bilen kör sin rödmarkerade sträcka.
Dvs undre bilen vinner.
okej, jag tror jag föstår. Om man skulle vilja förklara det med formel. Hur skulle det sett ut i så fall?
Mitt första resonemang går att översätta till Etot=Ek+Ep, kan du se hur? Det behöver vara generellt.
var är nollnivån i så fall? Eller vid början så kanske det finns både Ek och Ep men vid backen ökar Ep? Är det så man ska tänka?
Eller om man tänker så här:
Den övre bilen: ek vid utgångshastigheten med Ep, vid backen får vi både Ek och högre Ep och eftersom den mekaniska energin är konstant så blir Ek lägre än vid början. Efter kullen får vi Ek och Ep och då går det lika snabbt som början.
Vid den undre bilen: Ek och Ep vid utgången, vid gropen är det lägre Ep och därför går det snabbare då Ek får högre hastighet och vid det blåmarkerade får vi Ek + Ep igen.
Ja, precis. Nollnivån kan du sätta var du vill. Om du bara vill ha en positiv höjd kan du sätta den i gropens nedre kant.




