energi och rörelsemängd
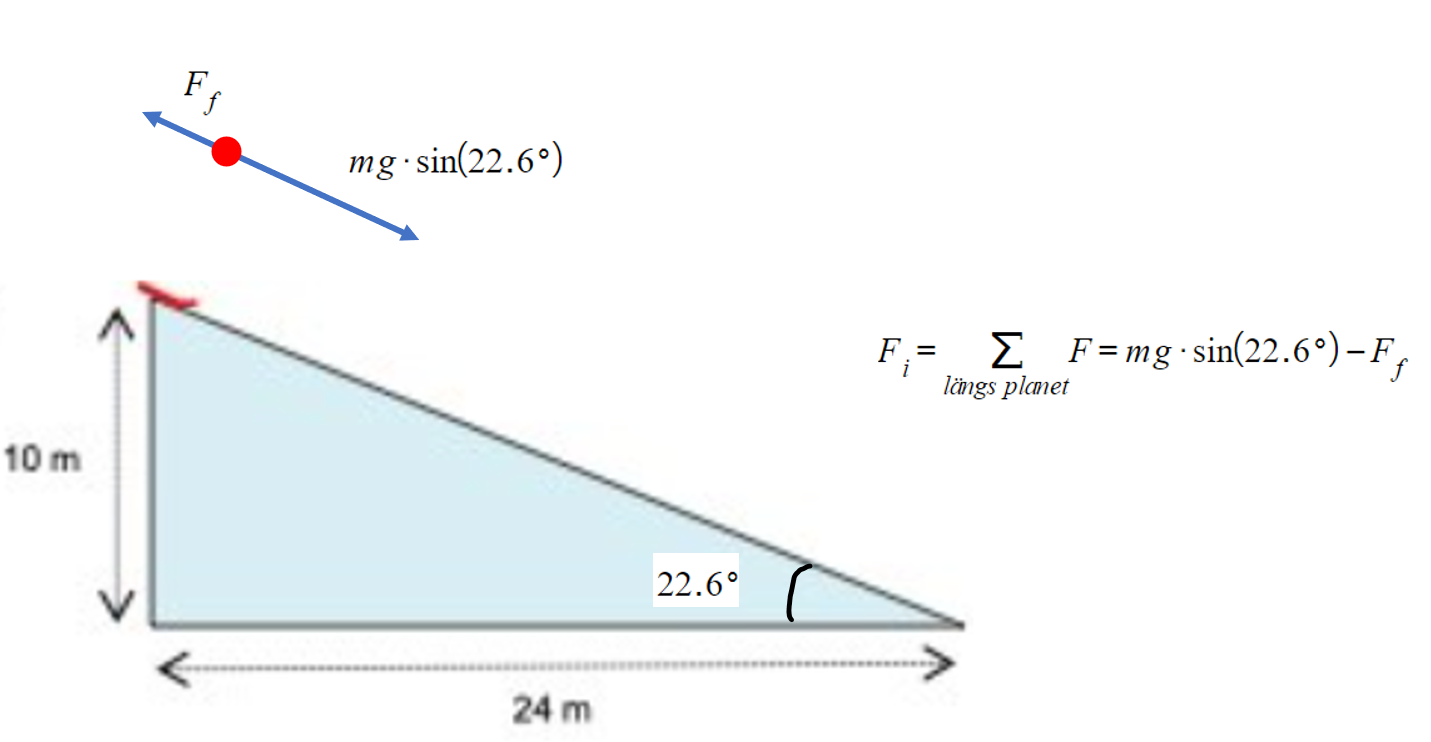
En pulka glider längs en lutande backe enligt figuren, Det tar 6,7 s att komma ner om pulkan startar från vila. Hur stor del av lägesenergin hos pulkan blir rörelseenergi?

Hur resonerar du kring uppgiften? Vad händer med den lägesenergi som inte blir rörelseenergi?
pulkan glider längs en lutande, för att räkna det ska jag använda w= F*s
kan jag säga att s= 10 m +24 m = 34 m nu har jag S
för att hitta F kan jag använda F = p/t
är det rätt?
Nä, du tänker lite fel, tror jag. Sträckan s som pulkan glider längs planet är inte 10+24=34m. Sträckan fås med hjälp av pythagoras sats, , eller hur? Och eftersom du inte vet sluthastigheten, därmed inte heller pulkans rörelsemängdsförändring, så kan du inte omedelbart räkna ut impulskraften med ditt lösningsförslag. Och visste du sluthastigheten så har du ju nästan redan löst uppgiften, eftersom lägesenergiförändringen är , och rörelseenergiförändringen är , och svaret på uppgiften är således . En lösningsstrategi verkar därför kunna vara att försöka räkna fram .
Fråga: Vad händer med den lägesenergi som inte blir rörelseenergi? Dvs varför kommer att bli mindre än ifall pulkan hade fallit fritt höjden ?
Bahga skrev:pulkan glider längs en lutande, för att räkna det ska jag använda w= F*s
kan jag säga att s= 10 m +24 m = 34 m nu har jag S
för att hitta F kan jag använda F = p/t
är det rätt?
Innan jag kan säga om ditt tankesätt är rätt eller fel så måste du berätta vad står för i din formel ovan.
(Sträckan som pulkan glider är 26m, inte 34m)
W är uträttade arbetet.
Ja, det är ett uträttat arbete, men det uträttas arbeten av flera olika krafter i uppgiften. Den viktiga iakttagelsen är att det är det uträttade arbetet av impulskraften som skapar rörelseenergi till pulkan (till skillnad från till exempel det uträttade arbetet av friktionskraften som blir energiförluster, dvs )
Om vi då fortsätter på ditt lösningsförslag,
och eftersom , blir
Hänger du med? Nu vet du pulkans sluthastighet, därmed kan du räkna fram hur stor del av lägesenergin som omvandlas till rörelseenergi .
Då kan jag säga att EL=F-Ek eller hur
Bahga skrev:Då kan jag säga att EL=F-Ek eller hur
Nä, det kan du inte. F är en kraft antar jag, den kan du inte jämföra med energiförändringar, det två olika storheter. Som att jämföra äpplen med päron.
Däremot kan du säga att lägesenergi blir friktionsarbete (värmeförluster) + kinetisk energi, dvs . Men för att lösa uppgiften behöver du inte räkna ut friktionskraften . Du behöver bara använda uttrycket för i kommentar #4, och sluthastigheten i kommentar #7 (ser nu att jag använde beteckningen för potentiell energi, och sedan använt som beteckning för samma sak)
s= 26m , och Ek= 3.9 joule eller hur?
men jag vet inte mg värdet för att F, är mg ett fast värdet?
Du kan inte räkna ut hur stor den kinetiska energin är, eftersom uppgifttexten berättar inte hur stor pulkans massa är. Därmed kan du heller inte räkna ut hur stor varken eller är. Uppgiften är inte heller att beräkna någon av dessa. Uppgiften är att beräkna hur stor del av lägesenergin som blir rörelseenergi. Det kan du göra utan att veta pulkans massa, bara du kan ta reda på pulkans sluthastighet.
Från kommentar #4 vet du att , genom att sätta in från kommentar #7 så kommer du fram till att
(Man kan också lösa uppgiften med hjälp av rörelseekvationerna för rörelse med konstant acceleration, dvsoch . Då behöver man inte använda sig av begreppen impuls, krafter och rörelsemängd)
Så slut svaret är 31
om jag säger att at2/2 då blir 7.8(6,7)2/2 = 175. 071 eller hur?
Ja, svaret borde vara 31%.
Nej du använder rörelselagen fel. Du vet inte pulkans acceleration innan du har räknat ut den.
Vi förutsätter att friktionskraften är konstant (precis som vi gjorde i #7), därmed har pulkan konstant acceleration nedför planet. Eftersom vi vet att pulkan accelererar på en sträcka av 26m och tid 6.7sek, så blir accelerationen
och sluthastigheten blir därmed
(jämför #7)
och du räknar ut lägesenergiförändring/rörelseenergiförändring på samma sätt som i #7.


