energi
En blykula med massan 0,40 kg faller likt figuren visar. Kulans potentiella energi sätts till noll då den befinner sig på den i figuren angivna nollnivån. I detta läge har den hastigheten 10 m/s. 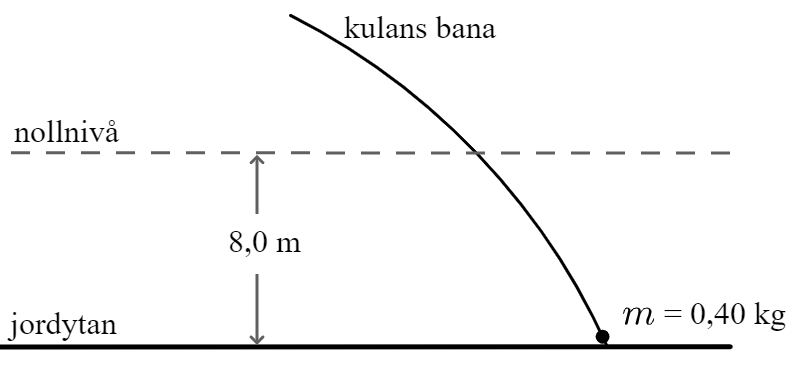 Hur stor är kulans totala energi 8,0 m under denna nollnivå, dvs strax ovanför jordytan? Luftfriktionen är försumbar.
Hur stor är kulans totala energi 8,0 m under denna nollnivå, dvs strax ovanför jordytan? Luftfriktionen är försumbar.
Jag började med att räkna ut rörelseenergin vid nollnivån och fick fram 20 J då (0.4*10^2)/2 blir 20 J
Då vet jag att den potentiella energin är 20 J också. Vid markytan är det röresleenergi och strax under nollnivån har vi mgh. Alltså 0.4*9.82*8 vilket blev 31.424 J. Borde inte rörelseenergin också vara 31.424 j?
och eftersomd et är straxt över jordytan så borde det bara vara rörelseenergin som räknas alltså 31.424 J?
Vid nollnivån har vi enbart rörelseenergi på 20 J.
När kulan sjunker under nollnivån förlorar den lägesenergi motsvarande mgh, som omvandlas till rörelseenergi. Totala energin är oförändrad
jag förstår inte. Under nollnivån finns det väl en höjd och man kan räkna ut mgh eller? Om man tänker att jag lyfte bollen från nollnivån till toppen och när jag släpper borde den inte fortsätta ner under nollnivån då jag bara har "lagrat" 20 J? blir det inte minus under nollnivån?
När kulan faller från nollnivån förlorar den lägesenergi, men vinner lika mycket rörelseenergi. Därför är totala energin oförändrad. Rörelseenergi+lägesenergi är konstant.
Det gäller även över nollnivån.
Anta att kulan släpps från stillastående från en höjd 5 m över nollnivån, då har den rörelseenergi = 0 och lägesenergin 5*0,4*10 (om g = 10) = 20 J. Totalt 0+20 J
När den når nollnivån har den förlorat lägesenergi 20 J men vunnit rörelseenergi 20 J summan är fortfarande 0+20 = 20 J
Man kan definiera sin nollnivå var som helst. Det är bara en referensnivå när man räknar. Tyngdkraften struntar i var vi definierat vår nolla, kulan faller till jordens centrum om inget stoppar den på vägen.


