Endimensionell rörelse

Jag tror att ditt uttryck för $L$ inte har dimensionen längd.

Pieter Kuiper skrev:

Jag tror att ditt uttryck för $L$ inte har dimensionen längd.

Tänkte att eftersom A reser sträckan L sätter jag den $s_1=L$och löser den som vanligt, men funkade väl inte. Kan man skriva om uttrycket på något sätt så det går? Eller bör jag försöka förstå detta istället (lärarens lösningsförslag):

Det här är säkert en bättre metod men jag vet själv att jag inte hade kommit på den, har lite svårt att få grepp om kinematik.

mekatronik skrev:

har lite svårt att få grepp om kinematik.

Börja med att göra en graf av bådas position som funktion av tid.

Pieter Kuiper skrev:

mekatronik skrev:

har lite svårt att få grepp om kinematik.

Börja med att göra en graf av bådas position som funktion av tid.

Detta bör väl stämma om jag inte har helt fel?

mekatronik skrev:

Detta bör väl stämma om jag inte har helt fel?

Bil A ska accelerera.

Pieter Kuiper skrev:

mekatronik skrev:

Detta bör väl stämma om jag inte har helt fel?

Bil A ska accelerera.

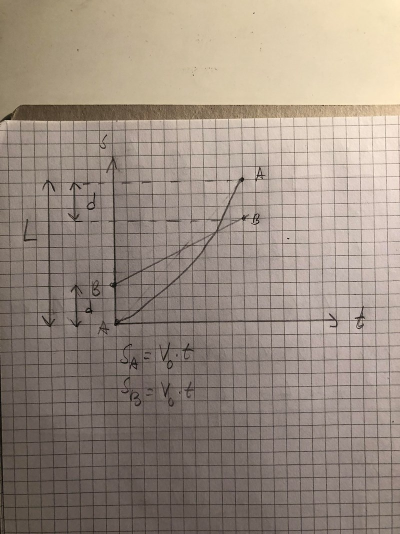
Juste, då kan inte grafen vara rät som jag har ritat. Då tänker jag att den bör se ut något sånt här (ignorera ekvationerna jag skrivit under grafen):

Men jag vet inte riktigt vad jag skall göra med denna info, ser inte riktigt hur L kan härledas.

mekatronik skrev:

Men jag vet inte riktigt vad jag skall göra med denna info, ser inte riktigt hur L kan härledas.

Det är i alla fall alltid en bra början i kinematiska uppgifter. Med korrekt ritning "ser" man hur kroppar rör sig. Med endast ekvationer är det större risk att något blir fel.

Jag tror att det hjälper att förstå lösningsförslaget.

I ritningen ska de båda ha samma fart vid t=0.

Pieter Kuiper skrev:

mekatronik skrev:

Men jag vet inte riktigt vad jag skall göra med denna info, ser inte riktigt hur L kan härledas.

Det är i alla fall alltid en bra början i kinematiska uppgifter. Med korrekt ritning "ser" man hur kroppar rör sig. Med endast ekvationer är det större risk att något blir fel.

Jag tror att det hjälper att förstå lösningsförslaget.

Har suttit med dessa uppgifter hela dagen och börjar bli lite trött nu, men tack för tipset jag skall försöka imorgon igen med den här grafen och förhoppningsvis kanske det sätter sig! :) 

Ett annat sätt att försöka lösa ut tiden är att utgå från bil B som inertialsystem.

Pieter Kuiper skrev:

Ett annat sätt att försöka lösa ut tiden är att utgå från bil B som inertialsystem.

Du tänker då att jag räknar $x_b$och sen tar det + 2d för att få fram L? 

Ja. Hur lång tid tar det för bil A att komma från ett avstånd d bakom bil B till ett avstånd d framför bil B när accelerationen är a? (från "stillastående" alltså)

Med ett hastighet - tid diagram får man ibland enklare samband. Även i detta fallet tycker jag.

mekatronik skrev:

Stoppar jag in detta i uttrycket får jag detta som är fel:

$L = \frac{v{\left(t\right)}^2}{2a}$

Nej, du får:

$L = \dfrac{ v^2-v_0^2}{2a}= \dfrac{(v+v_0)(v-v_0)}{2a}$

Detta är korrekt men du vet inte vad $v$ är lika med. Denna fart får du från:

$v = v_0 + at$

Tiden får du i sin tur från sträckan för den andra bilen:

$L -2d = v_0 t$

Kombinerar vi dessa tre ekvationer får vi en gröt av algebra:

$L= \dfrac{(2v_0+at)(at)}{2a}=t\cdot \dfrac{2v_0+at}{2}$

$L =\dfrac{L-2d}{v_0}\cdot \dfrac{2v_0+a\dfrac{L-2d}{v_0}}{2}$

$2L \cdot v_0 = 2L \cdot v_0-4d\cdot v_0 + a\dfrac{(L-2d)^2}{v_0}$

$4d\cdot v_0^2= a(L-2d)^2$

$\sqrt{\dfrac{4d}{a}}v_0 +2d=L$

V.S.V.

Som du ser är det Jan Ragnar visade oändligt mycket smidigare. Ha därmed för vana att göra både s/t-graf och v/t-graf.

Tillägg: 13 aug 2022 16:36

Något annat, som är lite bättre baserat på bilden du ritade, är helt enkelt att jobba med tiden hela tiden istället för att jobba tidlöst.

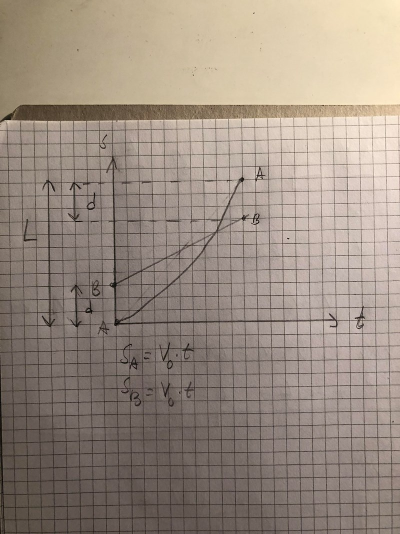
För bil A har vi enkelt att:

$s_A = v_0 t +at^2/2$

För bil B istället:

$s_B = v_0t$

Vi förstår genast från bilden ovan att:

$s_A = L$

$s_B = L-2d$

Resten är sedan klart...

SaintVenant skrev:

mekatronik skrev:

Stoppar jag in detta i uttrycket får jag detta som är fel:

$L = \frac{v{\left(t\right)}^2}{2a}$

Nej, du får:

$L = \dfrac{ v^2-v_0^2}{2a}= \dfrac{(v+v_0)(v-v_0)}{2a}$

Detta är korrekt men du vet inte vad $v$ är lika med. Denna fart får du från:

$v = v_0 + at$

Tiden får du i sin tur från sträckan för den andra bilen:

$L -2d = v_0 t$

Kombinerar vi dessa tre ekvationer får vi en gröt av algebra:

$L= \dfrac{(2v_0+at)(at)}{2a}=t\cdot \dfrac{2v_0+at}{2}$

$L =\dfrac{L-2d}{v_0}\cdot \dfrac{2v_0+a\dfrac{L-2d}{v_0}}{2}$

$2L \cdot v_0 = 2L \cdot v_0-4d\cdot v_0 + a\dfrac{(L-2d)^2}{v_0}$

$4d\cdot v_0^2= a(L-2d)^2$

$\sqrt{\dfrac{4d}{a}}v_0 +2d=L$

V.S.V.

Som du ser är det Jan Ragnar visade oändligt mycket smidigare. Ha därmed för vana att göra både s/t-graf och v/t-graf.

---

Tillägg: 13 aug 2022 16:36

Något annat, som är lite bättre baserat på bilden du ritade, är helt enkelt att jobba med tiden hela tiden istället för att jobba tidlöst.

För bil A har vi enkelt att:

$s_A = v_0 t +at^2/2$

För bil B istället:

$s_B = v_0t$

Vi förstår genast från bilden ovan att:

$s_A = L$

$s_B = L-2d$

Resten är sedan klart...

Om man utgår från bilden som Jan Ragnar har ritat, skall man då räkna integral för Va först och sedan för Vb, och sedan ta integral Vb-Va?