En uppgift jag minns från mitt Ma3c-kursprov om derivata och ekvationssystem.
Varje gång jag skriver ett prov och stöter på en uppgift som jag inte hinner med eller kan försöker jag minnas den så att jag kan lösa den i lugn och ro när jag kommer hem. Jag tog en gång ett matte 3c kursprov och stötte på en uppgift som jag inte kunde. Jag försökte sedan lösa den hemma men det gick inget vidare. Nu har jag liksom tagit matte 5 och kan fortfarande inte lösa den och jag vill få det, svart på vitt, ifall denna uppgift går att lösa algebraiskt, eller ifall jag missade någon detalj. Uppgiften lyder som följande:
Funktionen f(x) = 2x2 tangeras av två linjer i två punkter (se figur). De två tangerande linjerna skär varandra i punkten (-2;-42). Bestäm en av linjernas ekvation.
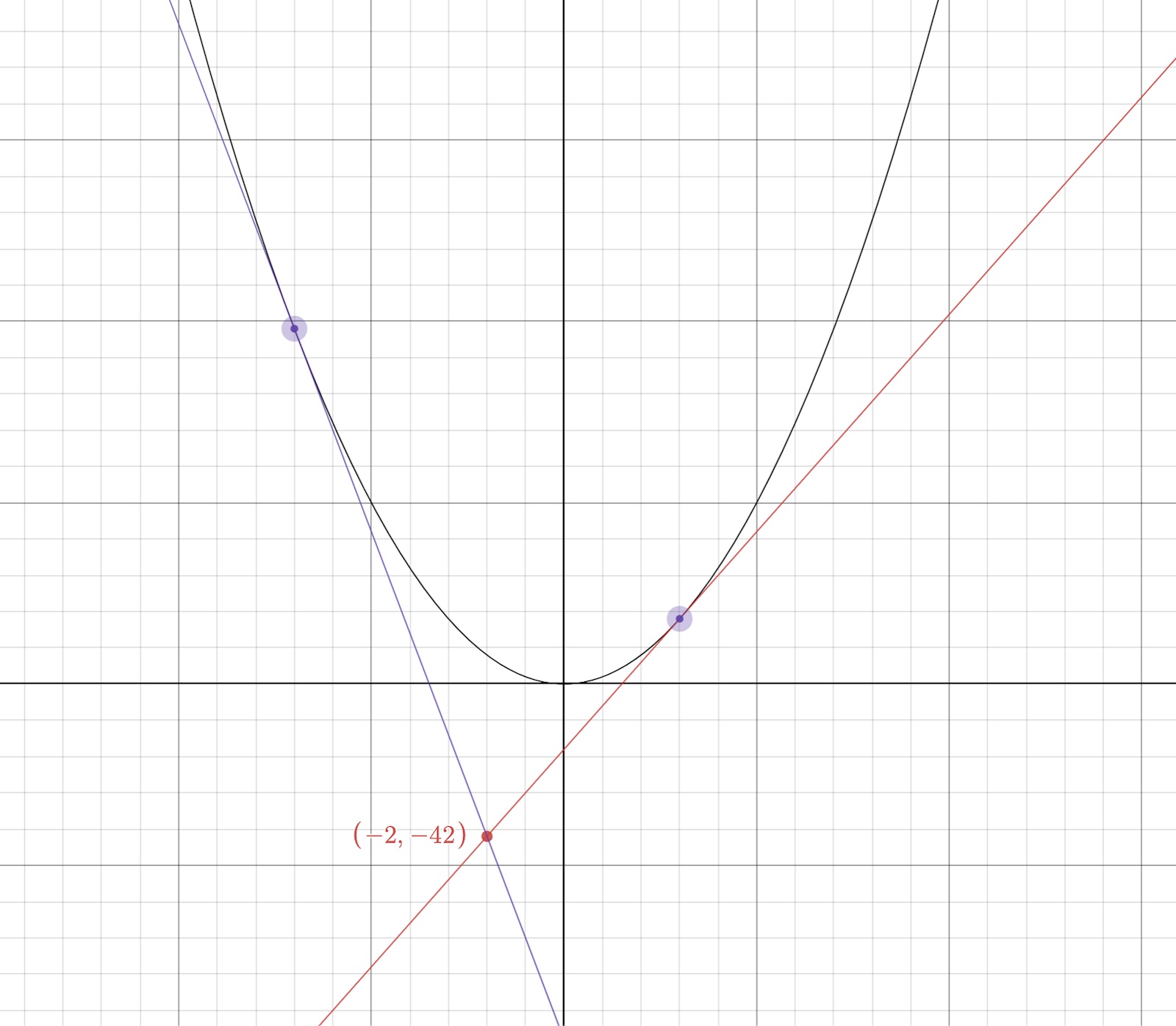Jag försökte ställa upp ett ekvationssystem för de två linjerna där den lila linjen (a) ges av k1x + m1 där k1 = f'(x1) = 8x1 ; Det vill säga:
a = 8x1x + m1
Den röda linjen (b) ges av k2x + m2; där k2 = f'(x2) = 8x2 ;
b = 8x2x+ m2
Ekvationssystemet ser då ut som följande:
-42 = -16x1 + m1
-42 = -16x2 + m2
Fyra okända? Det känns knappt som en matte 3c uppgift. Går den att lösa eller är det något som jag måste ha glömt? (Man ska inte kunna avläsa grafiskt)
För det första borde väl k-värdena ges av 4*x1 respektive 4*x2.
För det andra räckte det om man hittade en av de två linjerna.
För det tredje: om vi bara betraktar den lila linjen så ser vi att den så småningom kommer träffa y-axeln. Detta lär vara då y=m1. Vi vet även att då vi rör oss två punkter åt höger så rör vi oss k1*2 punkter neråt, så två punkter till höger om (-2,-42) kommer vi att hitta y-värdet -42-k1*2=m1. Gör samma sak för den röda linjen och du har fyra ekvationer med fyra okända variabler; detta lär vara lösbart.
Alternativt kan du skriva två uttryck för endera linjens k-värde.
Högerledet är kurvans derivata i tangeringspunkten (x1, 2x12)
(2x12 + 42)/(x1 + 2) = 4x1.
Löser du ekvationen får du x-värdena för båda tangeringspunkterna,
men du behöver bara den ena punkten.
Nu har du punkter och k-värde för endera linjen.
