En triangel
En triangel med arean 24 areaenheter begränsas av de positiva koordinataxlarna och en linje som går genom punkten (3,3). Bestäm linjens ekvation.
Fattar inte riktigt, skulle behöva lite hjälp på traven
jag vet inte hur man kan göra på denna
Börja med att rita ett koordinatsystem, markera den givna punkten och dra en linje genom den så att det bildas en triangel i första kvadranten.
Inför lämpliga namn på obekanta storheter.
Visa din bild.
Hej,
Arean för triangeln ges av basen gånger höjden delat med två.
Höjden på triangeln ges av m och bredden ges av x-koordinaten där räta linjen skär x-axeln, dvs där y=0.
Punkten (3, 3) och (0, m) används för att beräkna riktningskoefficenten:
k = (3-m)/(3-0) = (3-m)/3 = 1-m/3.
x-koordinaten där räta linjen skär y-axeln:
0=kx+m = (1-m/3)*x + m ger x = -m/(1-m/3) = 3m/(m-3).
Arean är x *m / 2 = 24. Sätt in x:
24 = m*3m/(m-3)/2 => 3 m^2 -48*m +48*3 = 0 vilket kan förenklas till m^2-48/3*m+48=0
Andragradsekvationen ger m1 = 4, m2 = 12. Motsvarande x-koordinater är x1 = 12 och x2 =4.
Två lösningar är möjliga. (1) y = -x/3+4 och (2) y=-3x+12
Arup skrev:jag vet inte hur man kan göra på denna
@Arup, det är inte tillåtet att bumpa sina inlägg inom 24h efter de postats.
/moderator
Mr P det gjorde jag inte. Jag frågae Peo-S på livehjälpen om hjälp och han sa att han skulle skicka lösning på tråden
Förstår inte riktigt. Oavsett så är ditt inlägg #2 en bumpning.
mitt försök
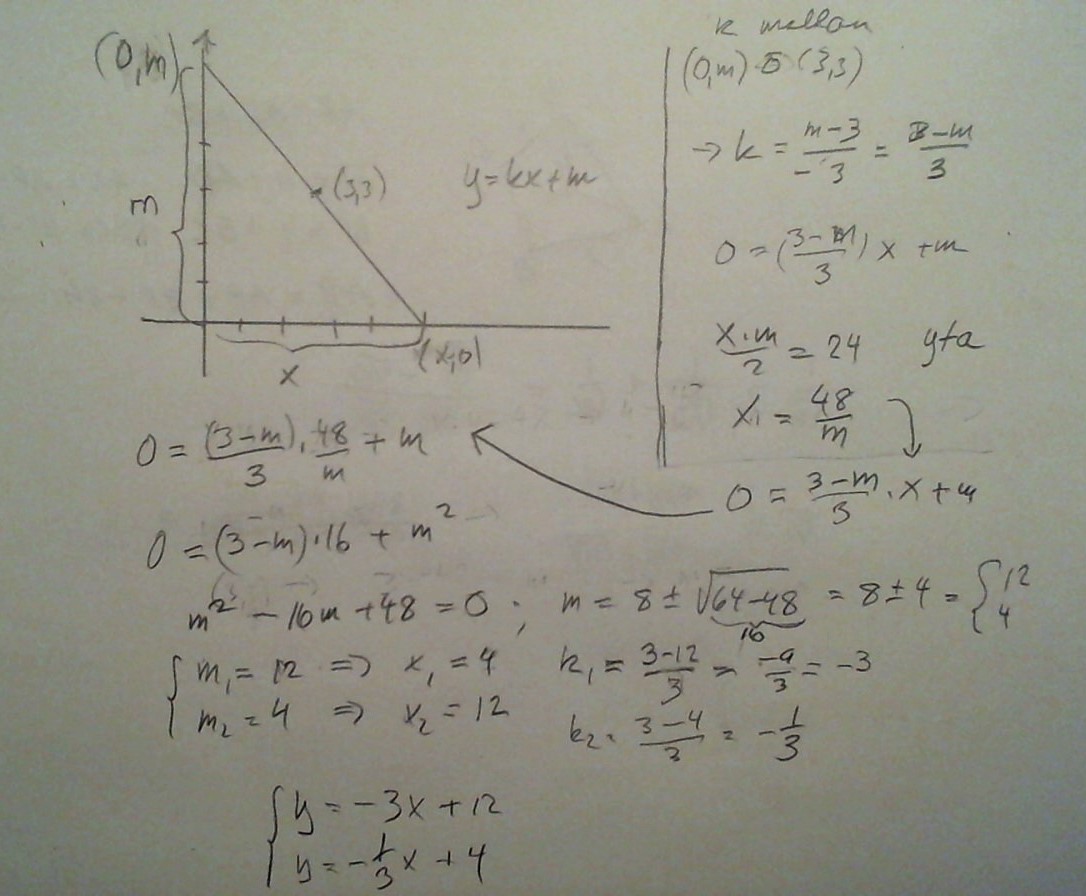
Det ser bra ut, men du kan gärna skriva mer text kring vilka samband du ställer upp och varför.
yngve jag är nyfiken på hur du löst den
Kan man tänka så här 
Ja, så kan du tänka.
Yngve skrev:Ja, så kan du tänka.
Är det rätt ?
Arup skrev:
Är det rätt ?
Ja, tankegången är rätt, men det är inte svar på frågan.
Från vem/vilka kommer lösningsförslagen i #8 och #11?
#11 är mitt egna och #8 fick jag hjälp på livehjälpen




