En textuppgift jag försöker förstå bättre.
Hej,
Den här textuppgiften försöker jag förstå bättre. Övar på gamla NP uppgifter inför mitt omprov. Har kommit till en uppgift som jag bara inte förstår riktigt. Försöker förstå texten, men jag förstår inte riktigt vad uppgiften säger för något. Det är en A uppgift, så den ska väl vara svårare.
Uppgiften:
En parabel har samma form som grafen till en andragradsfunktion.
Det finns parabler där x=f(y), dvs att parabeln ges av en andragradsfunktion f som är en funktion av y istället för x. Ge ex på en ekvation till en parabel med symmetrilinjen y=0.
Om jag tar det mening för mening:
"En parabel har samma form som grafen till en andragradsfunktion":
En parabel, det vet jag ju vad det är. Har samma form som grafen till en andragradsfunktion, okej det förstår jag, en andragradsfunktion är typ f(x)=x2 +4x+29där 29 är där parabelns ena typ "sida" blir skärningen med y axeln och där 4x med hjälp av PQ blir -2 som då är symmetrilinjen.
"Det finns parabler där x=f(y), dvs att parabeln ges av en andragradsfunktion f som är en funktion av y istället för x":
Det finns parabler där x=f(y), Vad är de här för något?
dvs att parabeln ges av en andragradsfunktion f, det här förstår jag inte alls?
som är en funktion av y istället för x" , en funktion av y ? istället för en funktion av x? De här vet jag inte riktigt vad som menas.
Vi kan se det som ett variabelbyte, du byter plats på x och y.
Ofta när vi skriver upp en funktion av tiden använder vi t som variabel istället för x. Detta är helt okej, eftersom att vi bara bytt ut variabeln från x till t. Vi skulle även kunnat döpa våra variabler "a" och "b" eller varför inte "äpple" och "päron".
Om du vill veta x som en funktion av y kommer x i detta fall vara variabeln som y brukar ta, och y är variabeln som x brukar vara. Funktionen x=f(y) är densamma som y=f(x) bara att vi har bytt namn på våra variabler.
Hej, tack för svaret.
Okej. Men om jag tar y=f(x) och ska skissa en graf utifrån bara detta. Då har jag ju fortfarande inget liksom att gå på. Jag vet att jag har y som är = funktionen x. Men jag har ju inget x värde så y=x vet jag inte hur jag skissar i en graf eller då y= funktionen x2. Så även om jag då tar x=f(y) dvs x är en funktion av y2 så kan jag inte "se i huvudet" hur en sådan här graf kan se ut riktigt.
ge ex på en ekvation till en parabel med symmetrilinjen y=0. Där x är en funktion av y, så x=y2 om y=0 så blir ekvationen x=02vart är y=0 vid origo, men där är x också 0... så om jag ritar en parabel börjar den från origo och hur vet man hur den liksom ska sträcka sig.?
Helt rätt, du behöver veta vad funktionen f är för att kunna rita ut grafen.
I nedanstånde bild har du först grafen till y=x2. Därifrån kan vi helt enkelt få grafen till x=y2 genom att antingen byta plats på koordinataxlarna (röd text i översta figuren) eller spegla grafen mot symmetrilinjen y=x (nedre grafen).
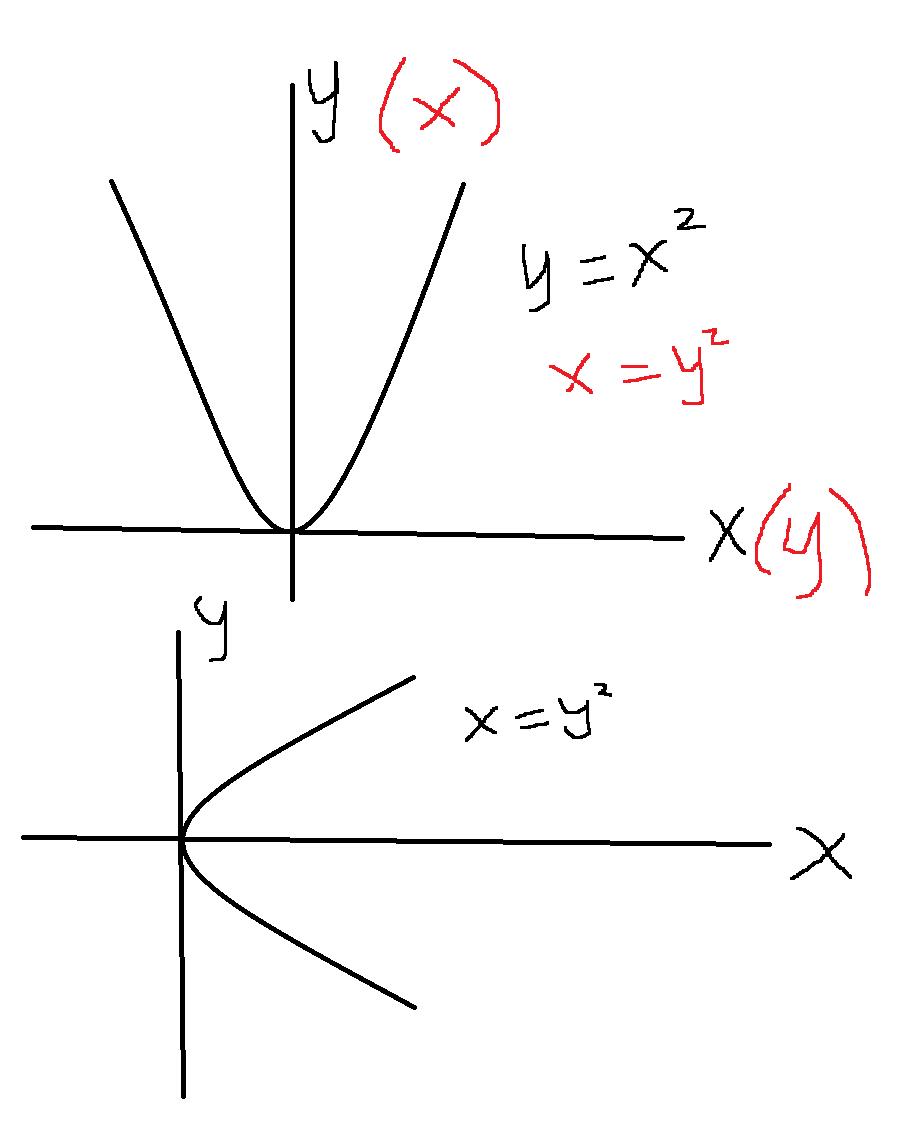
Jaha okej. Tack för skissen.
Så eftersom att jag inte vet vad funktionen f är, så.. kan jag inte riktigt rita ut en "exakt" eller "noga" graf. Men jag kan skissa ihop en graf som visar på hur en sådan graf kan se ut MEN den är inte exakt med exakta x, y värden. så.. om jag tittar på texten och det står:
"Det finns parabler där x=f(y)": så betyder det att man kan skissa en parabel som är "sträckt på "sidorna" av x axeln, istället för y axeln". Om y=0 så betyder det att parabeln "börjar" vid origo och sträcker sig längst med x axeln.
Och texten:
"Dvs att parabeln ges av en andragradsfunktion f som är en funktion av y istället för av x": De här betyder då bara funktion av y är: f(y), och istället för x är: f(x).
Så istället för att skriva en andragradsekvation som är y=x^2. Skriver man x=y^2 om det är en parabel måste ekvationen vara upphöjt och om symmetrilinjen ska vara 0. Varför skriver man då x=y2?
Det jag menar är, det betyder väl 1 dvs ett enkelt x räknas ju som 1 och om det är ombytt nu så borde väl y:et räknas som en 1:a med. Hur vet man att y är 0 här liksom och inte 1.
Hur vet du att ekvationen x=y^2 är en ekvation som visar på att symmetrilinjen är 0?
***
Ex hur hade de sett ut om uppgiften ville ha en ekvation till en parabel med symmetrilinje typ 4?
Det enklaste är att först byta ut alla variabler så att det blir den "vanliga" uppsättningen med y som funktion av x.
Frågan blir då: Ge exempel på en ekvation till parabeln med symmetrilinje x=0.
Detta vet du är t.ex. y=x^2, eller y=x^2+4.
Nu behöver du bara byta tillbaka x och y. Dvs svaret blir x=y^2 eller x=y^2+4 beroende på vilken funktion du valde.
Jag förstår men liksom, om du hade fått ekvationen x=y^2 eller y=x^2 hade du vetat då att y^2 respektive x^2 är 0
För om jag då tittar på y=x^2 +4 hur kan symmetrilinjen bli 4 här när y=x^2 har en symmetrilinje som är 0. y=x^2+4 har ju redan en symmetrilinje som då är 0?
Naturens skrev:För om jag då tittar på y=x^2 +4 hur kan symmetrilinjen bli 4 här när y=x^2 har en symmetrilinje som är 0. y=x^2+4 har ju redan en symmetrilinje som då är 0?
Stämmer, symmetrilinjen är 0.
Okej. Tror jag förklarar konstigt. Ledsen för alla frågor, men försöker bara förstå.
y=x^2 eller y=x^2+4 ger en symmetrilinje som är 0.
x=y^2 eller (antar jag att) x=y^2 +4 ger en symmetrilinje som är 0.
Så det jag har lite svårt för att förstå är.
Om y=0 så blir: x=y^2 = x=0^2.
Om jag skissar in denna ekvation in till ett koordinatsystem, så kan jag bara utgå från en punkt, dvs origo och sedan skissa en parabel "över och under" x axeln då ekvationen är x=y^2 och y är då 0.
Men låt säga att uppgiften bad om en ekvation till en parabel med symmetrilinjen y=4. Om y=4 så blir: x=y^2 som då är x=4^2.
vidare tänker jag okej. Om jag hade fått denna ekvation att skissa graf till hur hade jag tolkat den. x= betyder att parabeln "blir vänd" och 4^2 betyder det då att jag utgår från +4 på y axeln och "börjar där" så som jag i y=x^2 börjar från origo?


